The given diagram represents a screw gauge. The circular scale is divided into divisions and the linear scale is divided into millimeters. If the screw advances by when the circular scale makes complete revolutions, find the least count of the instrument and the reading of the instrument in the figure.
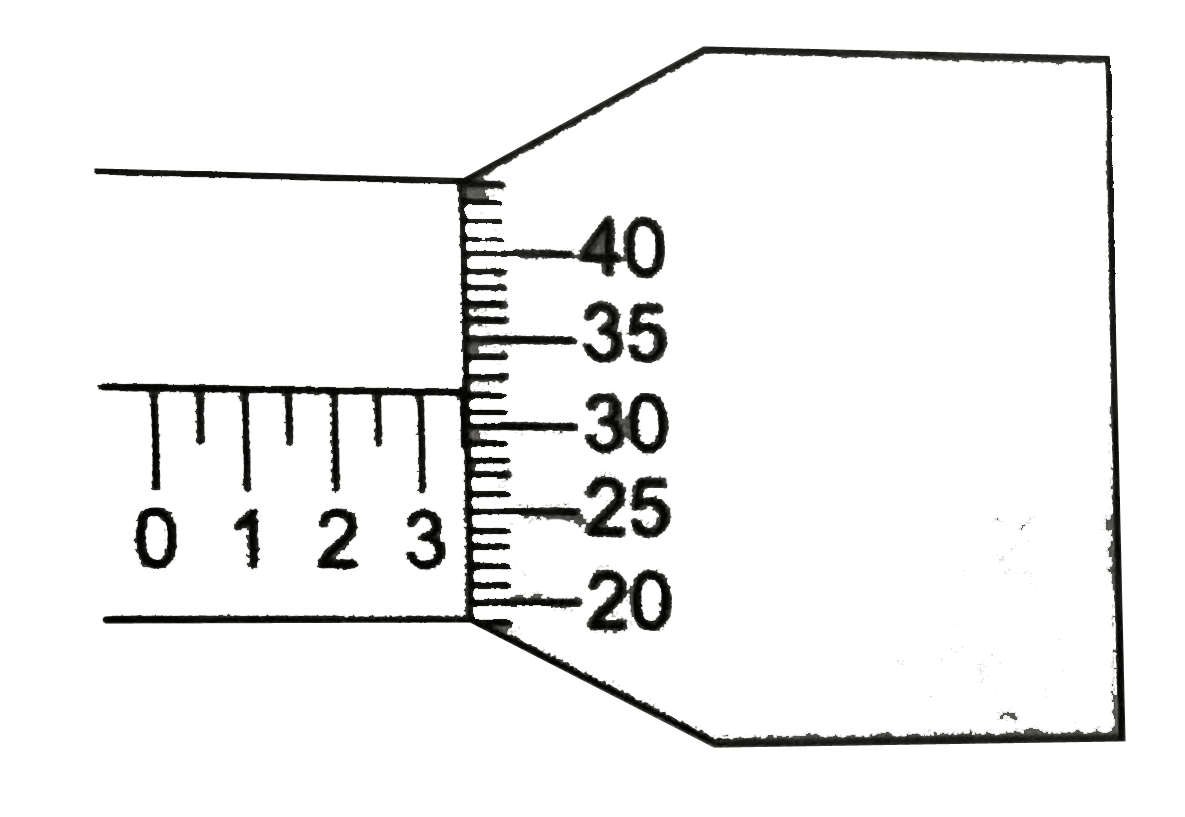 .
.
The correct Answer is:A, B, C
Pitch of the screw =
=
Least count =
=
Reading = Linear scale reading
+ (coinciding circular scale least count)
=
= .
Topper's Solved these Questions
Similar Questions
Knowledge Check
The circular scale of a screw gauge has 50 divisions and pitch of 0.5 mm. Find the diameter of sphere. Main scale reading is 2 -
_E01_289_Q01.png) A1.2B1.25C2.207D2.25
A1.2B1.25C2.207D2.25On six complete rotations, the screw gauge moves by 3 mm on the main scale. If there are 50 divisions on the circular scale the least count of the screw gauge is
A0.01 cmB0.02 mmC0.001 mmD0.001 cmCircular scale of a screw gauge moves through 4 divisions of main scale in one rotation. If the number of divisions on the circular scale is 200 and each division of the main scale is 1 mm., the least count of the screw gauge is
A0.01 mmB0.02 mmC0.03 mmD0.04 mm
Find the thickness of the wire The main scale division is of 1mm In a complete rotation the screw advances by 1mm and the circular scale has 100 devisions

View SolutionFind the thickess of the wire The main scale division is of 1mm In a complete rotation the screw advances by 1mm and the circular scale has 100 devisions Zero error of the screwgase is 0.007mm .
 .
.
View SolutionThe circular scale of a screw gauge has 50 divisions and pitch of 0.5 mm. Find the diameter of sphere. Main scale reading is 2.
View SolutionIn a screw gauge, the main scale has divisions in millimetre and circular scale has 50 divisions. The least count of screw gauge is
View SolutionThe pitch of a screw gauge is 1mm and its cap is divided into 100 divisions. When this screw gauge is used to measure the diameter of a wire, then main scale reading is 2mm and 58th division of circular scale coincides with the main scale. There is no zero error in the screw gage. Then the diameter of the wire is
View Solution


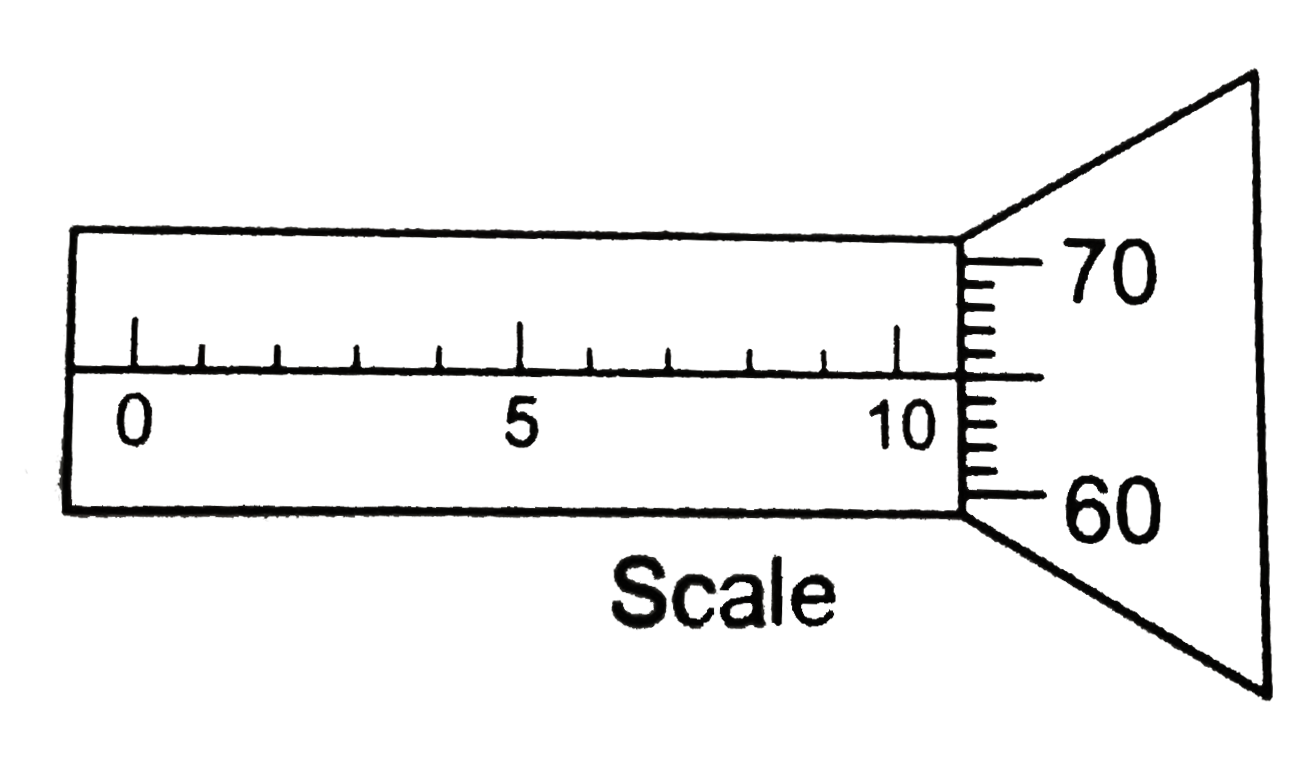 .
.