एक टायर बनाने वाली कम्पनी तय की गयी उन दूरियों का एक रिकॉर्ड रखती थी, जिसके पहले टायर बदलने की आवश्यकता पड़ी। निम्न सरणी में 1000 स्थितियों के परिणामों को दिखाया है।
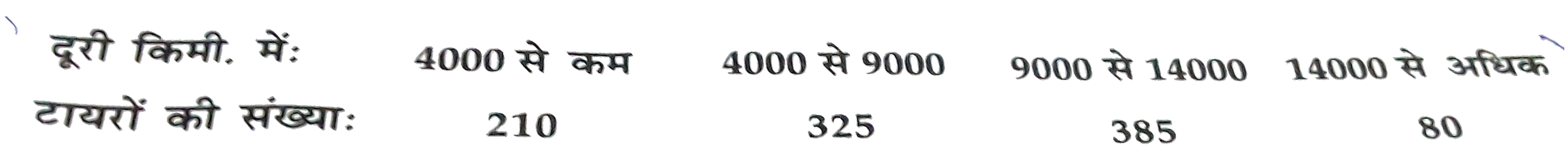
यदि आप इस कम्पनी से एक टायर खरीदते हैं, तो इस बात की प्रायिकता क्या होगी कि
(i)4000 किमी दुरी पूरी करने से पहले इसे बदलने की जरूरत होगी।
(ii ) यह 9000 किमी से भी अधिक की दुरी तक चलेगा।
(iii ) 4000 किमी. से 14000 किमी. के बीच कि दुरी तय करने के बाद इसे बदलना आवश्यक होगा।
(iv ) इसे बदलने की बिल्कुल भी आवश्यकता नहीं होगी।
(v ) इसे बदलने की आवश्यकता होगी।
अभिप्रयोगों कि कुल संख्या = 1000
(i ) 4000 किमी दुरी तय करने से पहले बदले गये टायरों की कुल संख्या = 210
∴ P (4000 किमी दुरी तय करने से पहले टायर बदलना आवश्यक हो ) =2101000=0.21
(ii ) 9000 किमी से अधिक दुरी तय करने के बाद बदलने वाले टायरों की संख्या =385+80=465
∴ P (टायर 9000 किमी से भी अधिक दूर तक चलेगा )=4651000=0.465
(iii ) 4000 किमी और 14000 किमी के बिच की कोई दुरी तय करने के बाद बदलने वाले टायरों की संख्या =325+385=710
∴ P (4000 किमी . और 14000 किमी . के बिच कोई दुरी तय करने के बाद टायर को बदलना आवश्यक हो )=7101000=0.71 ( iv ) उन टायरों की संख्या जिनकों बिल्कुल भी बदलने की आवश्यकता न हो = 0
∴ P (किसी भी टायर को बिल्कुल बदलना न हो ) =01000=0
(v ) चूँकि सभी टायरों को कभी न कभी बदलने की आवश्यकता होगी ।
∴ P (किसी भी टायर को बदलने की आवश्यकता होगी )=10001000=1
Topper's Solved these Questions
- प्रायिकता BOOK - RD SHARMACHAPTER - प्रायिकता EXERCISE - व्याख्यात्मक उदाहरण
1 Video
- प्रायिकता BOOK - RD SHARMACHAPTER - प्रायिकता EXERCISE - प्रश्नावली 25.1
12 Videos
- परिमेयकरण BOOK - RD SHARMACHAPTER - परिमेयकरण EXERCISE - बहु विकल्पीय प्रश्न
25 Videos
- बहुपदों का गुणनखण्डनBOOK - RD SHARMACHAPTER - बहुपदों का गुणनखण्डनEXERCISE - बहु विकल्पीय प्रश्न
20 Videos
Similar Questions
बीजों के 5 थैलों में से प्रत्येक थैले में से यदृच्छया 50 बीज चुनकर उन्हें ऐसी मानकीकृत अवस्थाओं में रखा गया जो अंकुरण के अनुकूल हैं। 20 दिन बाद प्रत्येक थैले से प्रत्येक संग्रह में अंकुरित हुए बीजों की संख्या गिनकर नीचे दर्शाए अनुसार एक सरणी में लिखी गई है।
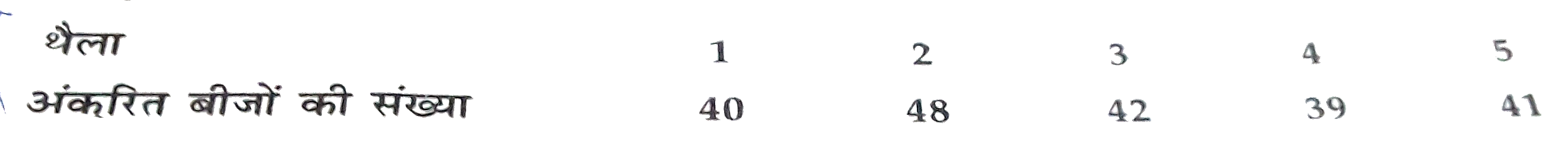
निम्नलिखित बीजों के अंकुरण की प्रायिकता क्या हैं?
(i ) एक थैले में 40 से अधिक बीज
(ii ) एक थैले में 49 बीज
(iii ) एक थैले में 35 बीज से अधिक बीज
(iv ) एक थैले में कम से कम 40 बीज
(v ) एक थैले में अधिकतम 40 बीज
View Solutionएक सिक्के को 1000 बार उछालने पर निम्नलिखित बारम्बारताएँ प्राप्त होती हैं :
चित :: 455, पट : 545
प्रत्येक घटना की प्रायिकता अभिकलित कीजिए ।
View Solution√10×√15 का मान होगा।
View Solutionयदि x2+3ax−2a का एक गुणनखण्ड x−2 हो, तो a =
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। इस बात की क्या प्रायिकता है की ग्यारह कदमो के पशचात वह व्यक्ति शुरुआती बिन्दु से एक कदम दूर है?
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। प्रायिकता ज्ञात कीजिए कि 5 कदम चलने के पश्चात, यह व्यक्ति प्रारम्भिक बिन्दु से एक कदम दूर है।
View Solutionएक अनभिनत पास को 6 बार उछाला जाता है। यदि एक समसंख्या प्राप्त करना एक सफलता है , तो
अधिक - से - अधिक 5 सफलताओ की प्रायिकता ज्ञात कीजिए।
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionयदि एक दीर्घवृत्त की दीर्घ अक्ष की लम्बाई, उसके लघु अक्ष की लम्बाई की तिगुनी है, तो उसकी उत्केन्द्रता होगी
View Solutionदो पासे n बार क्रमवार फेंके जाते हैं, कम से कम एक बार दो 6 प्राप्त करने की प्रायिकता होगी
View Solutionएक बिंदु p को एक वृत्त के भीतरी भाग से यादृच्छिक रूप से चयन किया जाता है, तो वह, प्रायिकता क्या होगी जिससे यह वस्तुतः वृत्त की परिसीमा के नजदीक होने की बजाय वृत्त के केंद्र से अधिक नजदीक होगा।
View Solutionएक कम्पनी द्वारा निर्मित 10% बल्व खराब निकलते हैं। 5 बल्बों के सैम्पल से किसी भी बल्ब की खराब न होने की प्रायिकता है
View Solutionएक घन के विकर्ण की लम्बाई 12√3 सेमी है। घन के कोर की लम्बाई .............होगी।
View Solution'आप चैन की नींद सो सकें इसलिए तो हम यहाँ पहरा दे रहे है' - एक फौजी के इस कथन पर जीवन - मूल्यों की दृष्टि से चर्चा कीजिए।
View Solutionएक थैले में 3 सफेद और 5 काली गेंदें हैं। थैले के अंदर से बिना देखे एक गेंद निकाली जाती है।
(a) एक सफेद गेंद प्राप्त करने की प्रायिकता क्या है?
(b) एक काली गेंद प्राप्त करने की प्रायिकता क्या है?
View Solutionअच्छी प्रकार से फेटी हुई 52 ताशों की एक गड्डी में से 1 बादशाह प्राप्त करने की प्रायिकता ज्ञात कीजिए।
View Solution
