दो सिक्कों को एक साथ 1000 बार उछाले पर हमें निम्न प्रणाम प्राप्त होते हैं:
दो चित : 210 बार
एक चित: 550 बार
कोई भी चित नहीं : 240 बार
इनमे से प्रत्येक घटना के घटने की प्रायिकता ज्ञात कीजिए।
हम घटनाओं को निम्न प्रकार से परिभाषित करते हैं :
A = दो चीतों का आना, B = एक चित का आना, C = कोई चित नहीं आना
अभिप्रयोगों की कुल संख्या = 1000
उन अभिप्रयोगों की संख्या घटना A घटित होती है = 210
उन अभिप्रयोगों की संख्या जिसमें घटना B घटित होती है = 550
उन अभिप्रयोगों की संख्या जिसमें घटना C घटित होती है = 240
∴ P(A)=उन अभिप्रयोगों की संख्या जिसमें घटना A घटित होती है कुल अभिप्रयोगों की संख्या =2101000=0.21
P(B)= उन अभिप्रयोगों की संख्या जिसमें घटना B घटित होती है कुल अभिप्रयोगों की संख्य=5501000=0.55
P(C)= उन अभिप्रयोगों की संख्या जिसमें घटना C घटित होती है कुल अभिप्रयोगों की संख्या=2401000=0.24
Topper's Solved these Questions
- प्रायिकता BOOK - RD SHARMACHAPTER - प्रायिकता EXERCISE - व्याख्यात्मक उदाहरण
1 Videos
- प्रायिकता BOOK - RD SHARMACHAPTER - प्रायिकता EXERCISE - प्रश्नावली 25.1
12 Videos
- परिमेयकरण BOOK - RD SHARMACHAPTER - परिमेयकरण EXERCISE - बहु विकल्पीय प्रश्न
25 Videos
- बहुपदों का गुणनखण्डनBOOK - RD SHARMACHAPTER - बहुपदों का गुणनखण्डनEXERCISE - बहु विकल्पीय प्रश्न
20 Videos
Similar Questions
बीजों के 5 थैलों में से प्रत्येक थैले में से यदृच्छया 50 बीज चुनकर उन्हें ऐसी मानकीकृत अवस्थाओं में रखा गया जो अंकुरण के अनुकूल हैं। 20 दिन बाद प्रत्येक थैले से प्रत्येक संग्रह में अंकुरित हुए बीजों की संख्या गिनकर नीचे दर्शाए अनुसार एक सरणी में लिखी गई है।
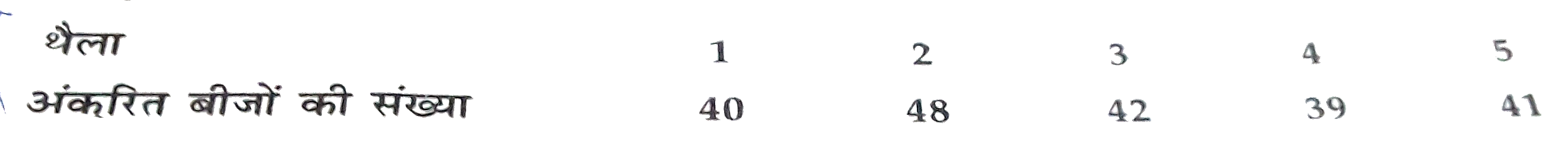
निम्नलिखित बीजों के अंकुरण की प्रायिकता क्या हैं?
(i ) एक थैले में 40 से अधिक बीज
(ii ) एक थैले में 49 बीज
(iii ) एक थैले में 35 बीज से अधिक बीज
(iv ) एक थैले में कम से कम 40 बीज
(v ) एक थैले में अधिकतम 40 बीज
View Solutionएक सिक्के को 1000 बार उछालने पर निम्नलिखित बारम्बारताएँ प्राप्त होती हैं :
चित :: 455, पट : 545
प्रत्येक घटना की प्रायिकता अभिकलित कीजिए ।
View Solution√10×√15 का मान होगा।
View Solutionयदि x2+3ax−2a का एक गुणनखण्ड x−2 हो, तो a =
View Solutionदो सिक्को को एक साथ 500 बार उछालने पर हमे यह प्राप्त होता है -
दो चित105बारएक चित275बारकोई भी चित नहीं120बार
इनमे से प्रत्येक घटना के घटने की प्रायिकता ज्ञात कीजिए ।
View Solutionयदि एक न्याय्य सिक्के को n बार उछाला गया हो , तो शीर्ष ( चित ) आने कि प्रायिकता p और पुच्छ (पट्ट ) आने कि प्रायिकता q हो तो ठीक 6 शीर्ष (चित ) आने कि प्रयिकता है -
View Solutionदो पासो को एक साथ चार बार फेका जाता है दोनों पासो पर प्राप्त अंको का योग 7 कम से कम दो बार आने की प्रायिकता ज्ञात कीजिए
View Solutionएक सिक्का n बार उछाला जाय तो सिद्ध कीजिए कि r से अधिक बार चित न आने कि प्रायिकता - (nC0+nc1+nC2+..........nc,)(12)n है
View Solutionएक सिक्के को तीन बार उछाला गया है। निम्न प्रत्येक अवस्था में P(AB) ज्ञात कीजिये - (i) A: तीसरी उछाल पर चित, B: पहली दोनों उछालों पर चित
(ii) A: कम से कम दो चित , B: अधिक्तम दो चित
(iii) A: अधिकतम दो पट , B: कम से कम एक पट
View Solutionछः सिक्के उछाले जाते है। केवल दो के चित आने कि क्या प्रायिकता है ?
View Solutionएक पासे को 7 बार उछालने पर तथ्यतः दो बार 5 आने कि प्रायिकता ज्ञात कीजिए ।
View Solutionएक व्यक्ति एक न्याय सिक्के को कितनी बार उछाले कि कम - से - कम एक चित आने कि प्रायिकता 90 % से अधिक हो ?
View Solutionतीन सिक्के एक साथ उछाले जाते यही , तब कम - से - कम एक चित आने की प्रायिकता होगी -
View Solutionएक सिक्के को तीन बार उछाला जाता है , यदि
E : न्यूनतम दो चित
F : अधिकतम दो चित, तो P(E/F) बराबर है -
View Solutionदो पासे n बार क्रमवार फेंके जाते हैं, कम से कम एक बार दो 6 प्राप्त करने की प्रायिकता होगी
View Solutionएक सिक्के को 10 बार उछाला जाता है ठीक 7 चित आने की प्रायिकता है
View Solution
