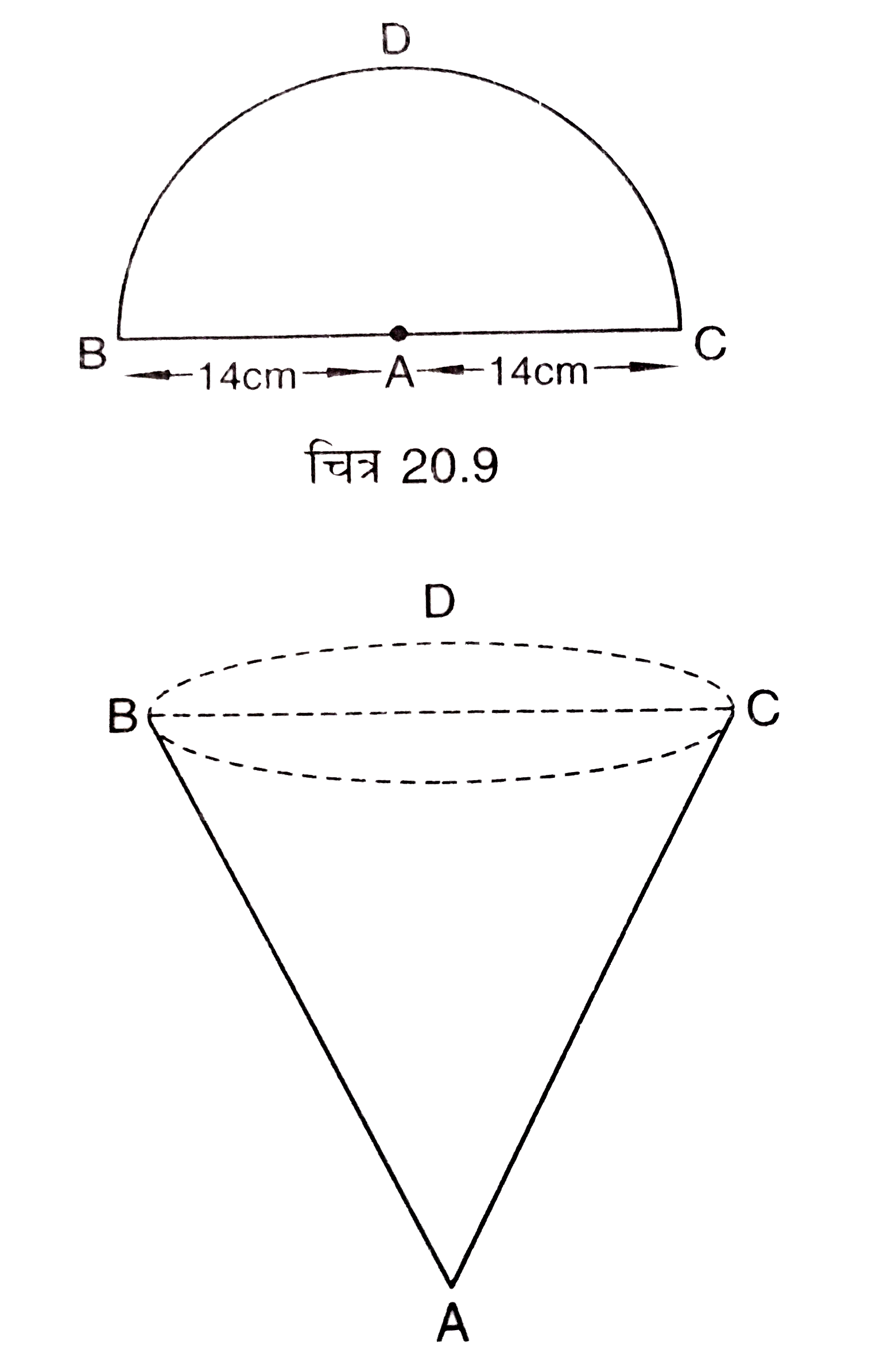
28 सेमी. व्यास की एक धातु की अर्द्ध - वृताकार चददर को एक खुले शंक्वाकार प्याले के रूप में मोड़ा जाता है । प्याले के रूप में मोड़ा जाता है। प्याले की गहराई तथा क्षमता ज्ञात कीजिए ।
622.26 cm3
522.26 cm3
122.26 cm3
322.26 cm3
The correct Answer is:A
जब अर्द्ध वृत्ताकार चददर को एक खुले शंक्वाकार प्याले के रूप में मोड़ा जाता है तो चददर की त्रिज्या प्याले की तिर्यक ऊँचाई बन जाती है तथा चददर की परिधि शंकु के आधार की परिधि बन जाती है।
∴ l= शंक्वाकार प्याले की तिर्यक ऊँचाई = 14 सेमी.
माना शंक्वाकार प्याले की त्रिज्या r सेमी. तथा ऊँचाई (गहराई ) h सेमी. है।
∵ शंक्वाकार प्याले के आधार की परिधि = चददर की परिधि
⇒ 2πr=π×14
⇒ r=7 सेमी.
अब, l2=r2+h2
⇒ h=√l2−r2
⇒ h=√142−72=7√3 सेमी.
⇒ h=(7×1.732) सेमी.=12.12 सेमी.
अतः प्याले की गहराई =12.12 सेमी.
स्पष्टतः प्याले की क्षमता = प्याले का आयतन
⇒ प्याले की क्षमता =13πr2hसेमी.3
=13×227×7×7×12.12 सेमी.3=622.26 सेमी.3
Topper's Solved these Questions
- लम्ब वृत्तीय शंकु का पृष्ठीय क्षेत्रफल तथा आयतन BOOK - RD SHARMACHAPTER - लम्ब वृत्तीय शंकु का पृष्ठीय क्षेत्रफल तथा आयतन EXERCISE - प्रश्नावली 20.1
23 Videos
- लम्ब वृत्तीय शंकु का पृष्ठीय क्षेत्रफल तथा आयतन BOOK - RD SHARMACHAPTER - लम्ब वृत्तीय शंकु का पृष्ठीय क्षेत्रफल तथा आयतन EXERCISE - प्रश्नावली 20.2
18 Videos
- लम्ब वृत्तीय बेलन का पृष्ठीय क्षेत्रफल तथा आयतन BOOK - RD SHARMACHAPTER - लम्ब वृत्तीय बेलन का पृष्ठीय क्षेत्रफल तथा आयतन EXERCISE - बहु विकल्पीय प्रश्न
19 Videos
- वास्तविक संख्याओं के घातांकBOOK - RD SHARMACHAPTER - वास्तविक संख्याओं के घातांकEXERCISE - बहु विकल्पीय प्रश्न
40 Videos
Similar Questions
यदि एक शंकु की ऊँचाई 60 सेमी. और इसके आधार की त्रिज्या 21 सेमी. है, तो उसका वक्र पृष्ठीय क्षेत्रफल ज्ञात करो ।
View Solutionउस लम्ब वृत्तीय शंकु का आयतन ज्ञात कीजिए, जिसकी :
त्रिज्या 6 सेमी. और ऊँचाई 7 सेमी. है।
View Solutionकिसी बेलन की त्रिज्या दुगनी व ऊंचाई आधी करने पर इसके वक्र पृष्ठ का क्षेत्रफल होगा :
View Solution{2−3(2−3)3}3 का मान होगा:
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionएक पुस्तक की मोटाई 2 सेमी है और इसमें 800 पृष्ठ है। एक पृष्ठ की मोटाई मानक रूप में ज्ञात कीजिए।
View Solutionजब धातु M को NaOH के साथ उपचारित किया जाता है, तो एक श्वेत जिलेटिन जैसा अवक्षेप 'X' प्राप्त होता है, जो NaOH के आधिक्य में घुलनशील होता है। यौगिक 'X' प्रबल रूप से गर्म करने पर एक ऑक्साइड देता है जिसका उपयोग वर्णलेखिकी में एक अधिशोषक के रूप में किया जाता है। धातु 'M' है:
View Solutionएक प्रबल अम्ल की उपस्थिति में एक ऑक्सीम के एक एमाइड में पुनर्विन्यास को कहा जाता है:
View SolutionCIF_4^(+) में केंद्रीय रूप के चारों ओर की आकृति है:
View Solutionसंगलित अशुद्ध धातु को लकड़ी के हरे रंग के लट्टे के साथ हिलाकर फफोलेदार तांबा को परिष्कृत किया जाता है, क्योंकि इस प्रकार की लकड़ी, हाइड्रोकार्बन गैसों (जैसे CH_4 ) को मुक्त करती है। इस प्रक्रम X को ________ कहा जाता है और इसका उपयोग धातु में प्रारंभ में उपस्थित Y की अशुद्धियों के शुद्धिकरण के लिए किया जाता है। Y _______ है।
View Solutionएक अभिक्रिया में, जब अभिकारक की प्रारंभिक सांद्रता एक-चौथाई तक कम की जाती है, तो अर्द्ध अभिक्रिया को पूर्ण करने के लिए आवश्यक समय 16 गुना बढ़ जाता है। अभिक्रिया की कोटि क्या होगी?
View Solutionरेसिमिक मिश्रणों के d तथा । प्रतिबिंब समावयवियों में पृथक्करण की प्रक्रिया को कहा जाता है :
View Solutionएक संकुल में केंद्रीय धातु परमाणु की उपसहसंयोजन संख्या को किसके द्वारा प्रदर्शित किया जाता है?
View Solutionएक युक्ति जो हाइड्रोजन और मेथेन जैसे ईंधनों की दहन ऊर्जा को सीधे विद्युत ऊर्जा में परिवर्तित करती है, उसे किस रूप में जाना जाता है?
View Solutionबाइथायोनल को किसकी तरह कार्य करने के लिए सामान्यतः साबुन में एक योज्य के रूप में मिलाया जाता है
View Solutionनिम्नलिखित में से किस औषधि का उपयोग एक पीड़ाहारी के रूप में किया जाता है?
View Solution
