समांतर चतुर्भुज ABCD में भुजाओं AB तथा BC पर कोई दो बिंदु क्रमशः E तथा F है, सिद्ध कीजिए कि ar(ΔADF)=ar(ΔDCE).
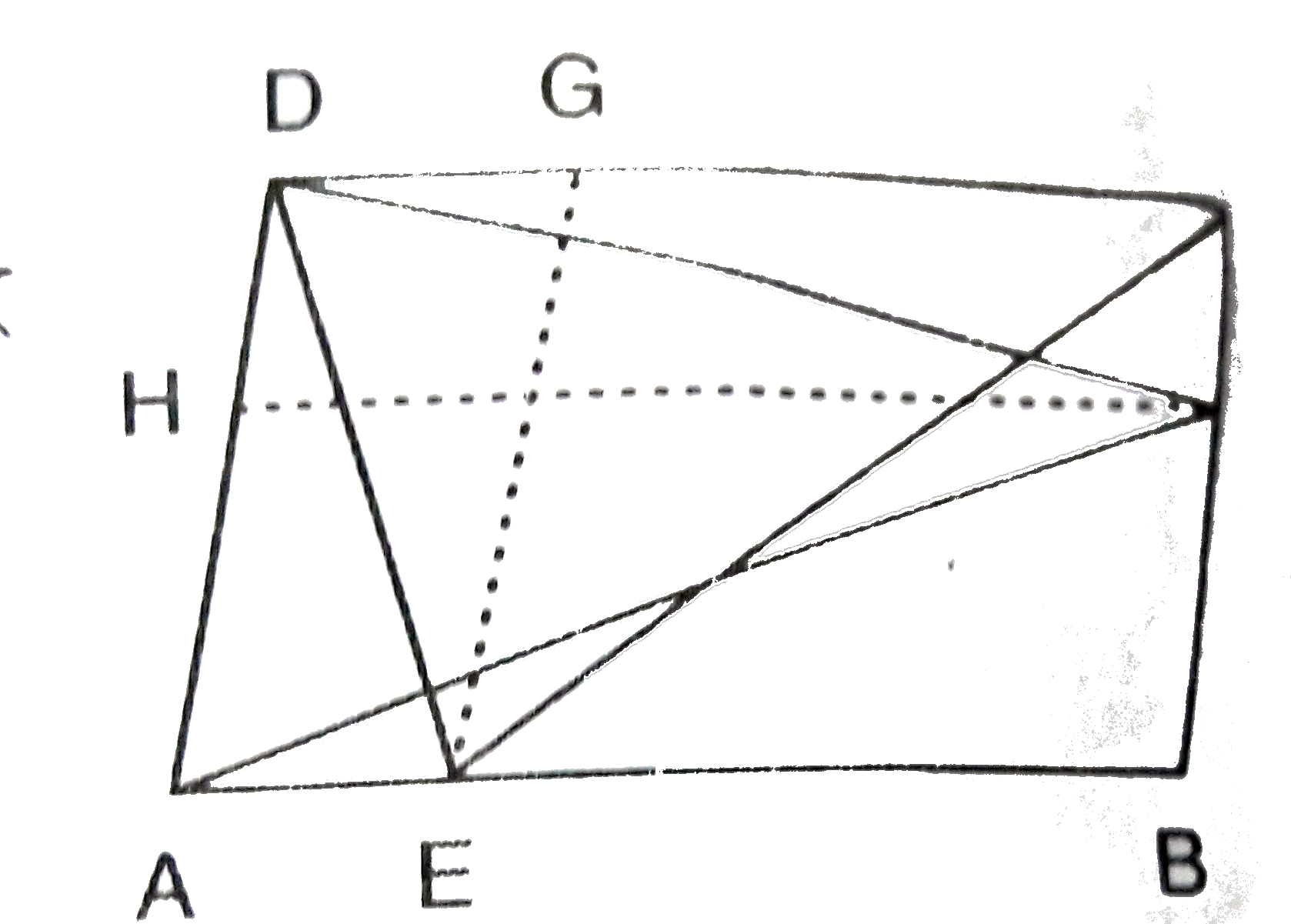
रचना : EG ।। AD तथा FH ।। AB खींचिये।
उपपत्ति : चूँकि FH ।। AB ( रचना से ) । अतः ABFH एक समांतर चतुर्भुज है।
चूँकि AF समांतर चतुर्भुज ABFH का एक विकर्ण हैं।
∴ar(ΔAFH)=12ar(||gmABFH) ...(i)
इसी प्रकार DF समांतर चतुर्भुज DCFH का एक विकर्ण है।
∴ar(ΔDFH)=12ar(||gmDCFH) ...(ii)
(i ) तथा (ii ) से,
ar(ΔAFH)+ar(ΔDFH)=12ar(||gmABFH)+12ar(||gmDCFH)
⇒ar(ΔAFH)+ar(ΔDFH)=12[ar(||gmABFH)+(ar(||gmDCFH)]
⇒ar(ΔAFH)+ar(ΔDFH)=12ar(||gmABCD)
⇒ar(ΔADF)=12ar(||gmABCD) ...(iii)
||gm AEGD में, DE एक विकर्ण है।
∴ar(ΔDEG)=12ar(||gmAEGD) ...(iv)
||gm CBEG में, CE एक विकर्ण है।
∴ar(ΔCEG)=12ar(||gmCBEG) ...(v)
(iv ) तथा (v ) से,
ar(DEG)+ar(ΔCEG)=12(||gmAEGD)+12ar(||gmCBEG)
⇒ar(DEG)+ar(ΔCEG)=12[ar(||gmAEGD)+ar(||gmCBEG)]
⇒ar(DEG)+ar(ΔCEG)=12[ar(||gmABCD)]
⇒ar(ΔDCE)=12ar(||gmABCD) ...(vi)
(iii ) तथा (vi ) से,
ar(ΔADF)=ar(ΔDCE)
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:व्याख्यात्मक उदाहरण
Explore 1 Video
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नावली 15.1
Explore 6 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण Book:RD SHARMAChapter:संख्यिकीय आंकड़ों का आलेखीय निरूपण Exercise:बहु विकल्पीय प्रश्न
Explore 8 Videos
- सर्वांगसम त्रिभुजेंBook:RD SHARMAChapter:सर्वांगसम त्रिभुजेंExercise:बहु विकल्पीय प्रश्न
Explore 17 Videos
Similar Questions
चित्र में , P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिंदु है दर्शाइए कि
(i) ar(ΔAPB)+ar(ΔPCD)=12ar(।।gmABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)

View Solutionआकृति में आकृति एक ही आधार तथा समान समांतर रेखाओं के बीच स्थित है :

View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
View SolutionA point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar(ΔADF)=ar(ABFC).
View Solutionयदि ΔABC~ΔPQR तथा BC=5QR तो ar(ΔABC):ar(ΔPQR) है
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
View Solutionयदि किसी चतुर्भुज की भुजाओं को क्रमानुसार दिशा व परिमाण में निरूपित करने वाले सदिश ¯a,¯b,¯c,¯d हों तों सिद्ध कीजिए कि चतुर्भुज एक समांतर चतुर्भुज होगा यदि और केवल यदि ¯a+¯c=¯0 जिससे ¯b+¯d=¯0
View Solutionकिसी समांतर चतुर्भुज ABCD में यदि −−→AB=¯a तथा −−→BC=¯b तो सिद्ध कीजिए कि
−−→AC=¯a+¯b और −−→BD=¯b−¯a.
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionयदि समान्तर चतुर्भुज कि दो आसान भुजाएँ →a तथा →b हो , तो इसका विकर्ण ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि बिन्दु (2,0),(11,6) तथा (−4,−4) समरेख है।
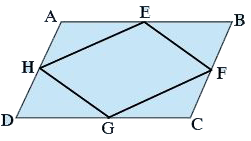
View SolutionIf E, F G and H are respectively the midpoints of the sides AB, BC, CD and AD of a parallelogram ABCD, show that ar(EFGH) =12 ar (ABCD) .
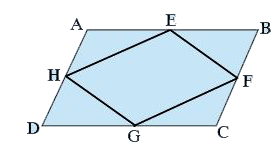
View SolutionIf E, F G and H are respectively the midpoints of the sides AB, BC, CD and AD of a parallelogram ABCD, show that ar(EFGH) =12 ar (ABCD) .
View Solution

