सिद्ध कीजिए कि उन सभी समान्तर चतुर्भुज में जिनकी भुजायें दी हुए है, आयत का क्षेत्रफल सबसे अधिक होता है।

Video Solution

Text Solution

Verified by Experts

मान लीजिये ABCD एक समान्तर चतुर्भुज है जिसमे AB = a तथा AD = b है। माना आधार AB की संगत ऊँचाई h है।
$∴ a r ({||}^{g m} A B C D) = A B \times h = a h$
चूँकि भुजायें a तथा b दी हुई हैं। अतः समान भुजाओं a तथा b वाले हम अनंत समान्तर चतुर्भुज बना सकते है। जिनकी ऊँचाइयाँ भिन्न-भिन्न हों।

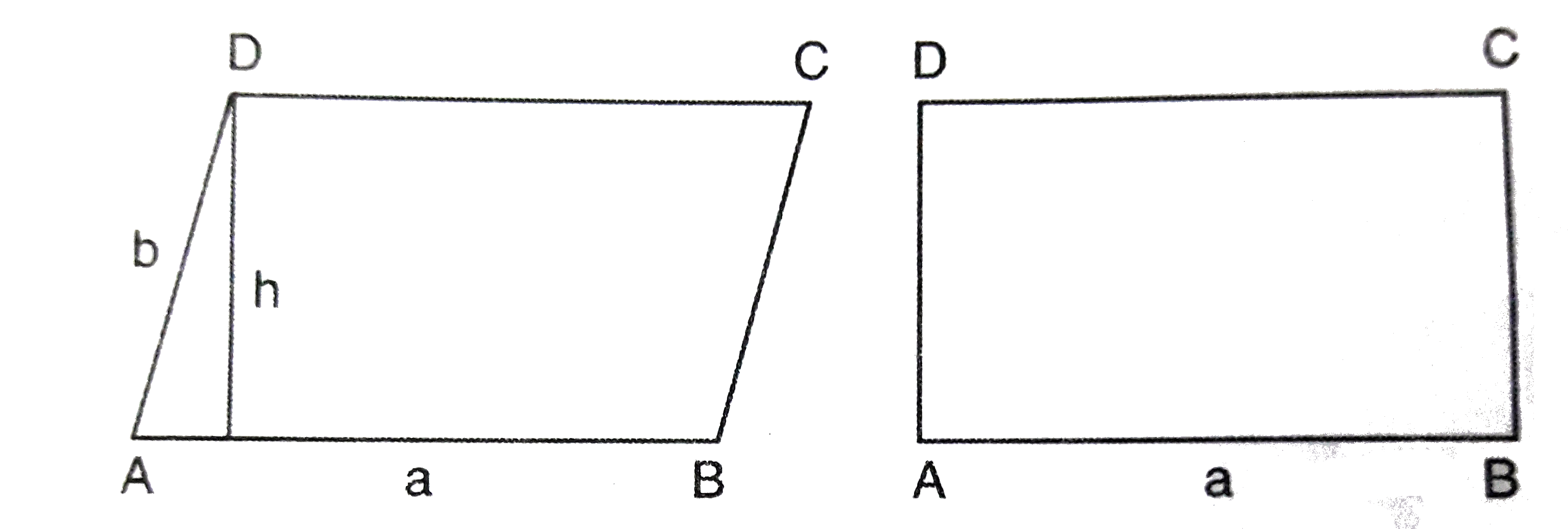
अब, $a r ({||}^{g m} A B C D) = a h$
$\Rightarrow a r ({||}^{g m} A B C D)$ अधिकतम तभी होता जब h अधिकतम है। [ $∵$ a दिया है अर्थात a स्थिर है]
परन्तु h द्वारा प्राप्त किया जा सकने वाला अधिकतम मान AD = b है। लेकिन यह तब ही सम्भव है जबकि घुजा AD , भुजा AB पर लम्ब हो अर्थात ${||}^{g m}$ ABCD के आयत हो।
अतः $a r ({||}^{g m} A B C D)$ अधिकतम तभी होता जब $A D ⊥ A B$ अर्थात जब ${||}^{g m}$ ABCD , एक आयत हो।

|

Updated on:21/07/2023

Class 9 MATHS AREA OF PARALLELOGRAMS AND TRIANGLES

Topper's Solved these Questions

Similar Questions

RD SHARMA-समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल -बहु विकल्पीय प्रश्न

Home
Ask Doubt
Profile