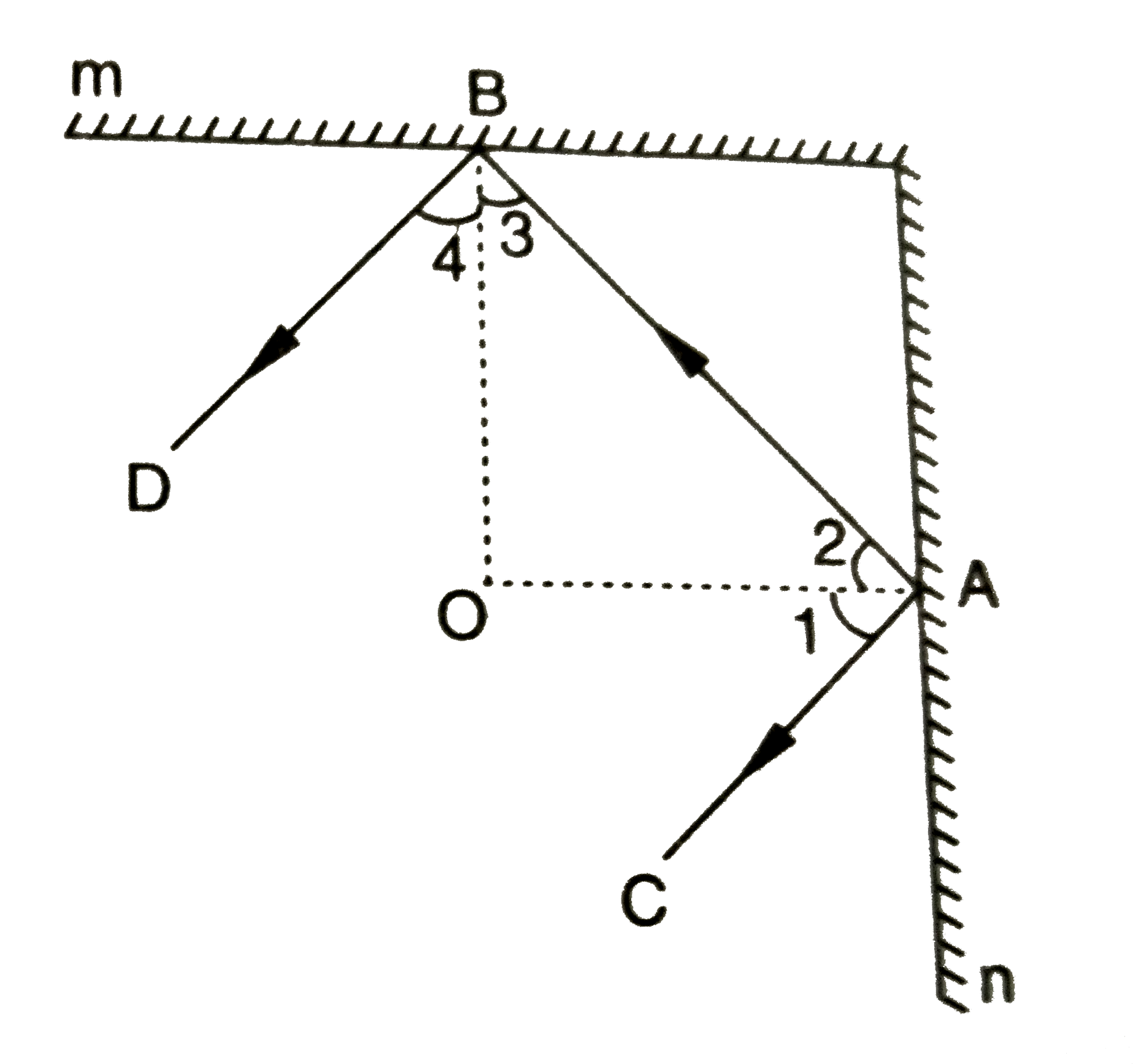
चित्र में, m तथा n परस्पर दो लंबवत समतल दर्पण है। प्रदर्शित कीजिए कि आयतित किरण CA, परावर्तित किरण BD के समान्तर है।
यह सिद्ध करने के लिए कि CA || BD हमे यह सिद्ध करना पर्याप्त होगा कि
∠CAB+∠ABD=180∘
चूँकि दर्पण m तथा n परस्पर लम्ब है एवम OB तथा OA क्रमशः m तथा n पर लम्ब है। अतः
OA⊥OB⇒∠BOA=90∘
ΔBOA में कोण योग गुणधर्म लगाने पर
⇒∠2+∠3+∠BOA=180∘
⇒∠2+∠3+90∘=180∘ [∵∠BOA=90∘]
⇒∠2+∠3=90∘
⇒2(√2+√3)=180∘ [दोनों पक्षों को 2 से गुणा करने पर]
⇒2(√2)+2(√3)=180∘
⇒∠CAB+∠ABD=180∘ [∵ आयतन का कोण = परावर्तन कोण ∴∠1=∠2 तथा ∠3=∠4 ⇒2∠2=∠CAB तथा 2∠3=∠BAD]
अतः दो रेखायें CA तथा BD एक तिर्यक रेखा AB द्वारा इस प्रकार प्रतिच्छेदित होती है कि ∠CAB+∠ABD=180∘ अर्थात AB के एक ही ओर स्थित अन्तः कोणों का योगफल 180∘ है। अतः CA || BD.
Topper's Solved these Questions
- त्रिभुज तथा उसके कोण Book:RD SHARMAChapter:त्रिभुज तथा उसके कोण Exercise:प्रश्नावली 9.1
Explore 17 Videos
- त्रिभुज तथा उसके कोण Book:RD SHARMAChapter:त्रिभुज तथा उसके कोण Exercise:प्रश्नावली 9.2
Explore 28 Videos
- चतुभुर्ज Book:RD SHARMAChapter:चतुभुर्ज Exercise:बहु विकल्पीय प्रश्न
Explore 32 Videos
- दो चरो वाले रैखिक समीकरण Book:RD SHARMAChapter:दो चरो वाले रैखिक समीकरण Exercise:बहु विकल्पीय प्रश्न
Explore 10 Videos
Similar Questions
एक ΔABC में, यदि ∠A=55∘,∠B=40∘, तो ∠C ज्ञात कीजिए।
View Solutionयदि किसी त्रिभुज के आधार को दोनों दिशाओं में आगे बढ़ाने पर प्राप्त बहिष्कोणो के मान 104∘ तथा 136∘ है, तो त्रिभुज के सभी कोण ज्ञात कीजिए।
View Solutionकिसी चतुभुर्ज में सम्मुख भुजाओं के लिए
View Solutionयदि (4,19) समीकरण y=ax+3 का एक हल है तो , a का मान है:
View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
View Solutionचित्र में AB ,BC तथा CA वृत्त कि स्पर्श रेखाएं है। यदि BC=6.3 सेमी तथा MC=2.7 सेमी हो ,तो BL कि नाप लिखिए।

View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionयदि दो रेखाओ के दिक् अनुपात a1,b1,c1 तथा a2,b2,c2 है तो वे परस्पर लंबवत होगी, यदि -
View Solutionदो परस्पर लंबवत रेखाओ के दिक् अनुपात 1,2,3 तथा 3,2,λ है, तो का मान लिखिय।
View Solutionयदि समान्तर चतुर्भुज कि दो आसान भुजाएँ →a तथा →b हो , तो इसका विकर्ण ज्ञात कीजिए।
View Solutionदो रिक्त स्थानों के लिए A एवं B दो उम्मीदवार है । A के चुने जाने कि प्रायिकता 13 तथा B के चुने जाने कि प्रायिकता 15 है। निम्न कि प्रायिकता ज्ञात कीजिए :
कोई भी चुना न जाये
View Solutionयदि दीर्घवृत्त 4x2+y2=8 के बिन्दुओ (1,2) तथा (a,b) पर खींची गई स्पर्श रेखाएं परस्पर लंबवत है, तो a2 बराबर है
View Solutionयदि बिन्दु (2,α,β) उस समतल पर स्थित है, जो बिन्दुओ (3,4,2) तथा (7,0,6) से होकर जाता है तथा समतल 2x−5y=15 के लंबवत है, तो 2α−3β बराबर है
View Solutionx-अक्ष के समान्तर समतल का समीकरण है
View Solutionनिम्न कथन सत्य है या असत्य-
Y -अक्ष के समान्तर समतल समीकरण ax+by+d=0 है।
View Solutionरेखा क्या है ? रेखाखण्ड क्या है ? किरण क्या है ? आओं सीखें
View Solution