यदि बहुपद f(x)=x4−6x3−26x2+138x−35 के दो शून्यक 2±√3 है, तो अन्य शून्यक ज्ञात कीजिये |
चूँकि 2+√3 और 2−√3 बहुपद f(x) के दो शून्यक है |
∴{x−(2+√3)}{x−(2−√3)}
=(x−2−√3)(x−2+√3)
=(x−2)2−(√3)2=x2−4x+1,f(x) का एक गुणनखण्ड है |
अतः बहुपद f(x) को x2−4x+1 से विभाजित करते है |
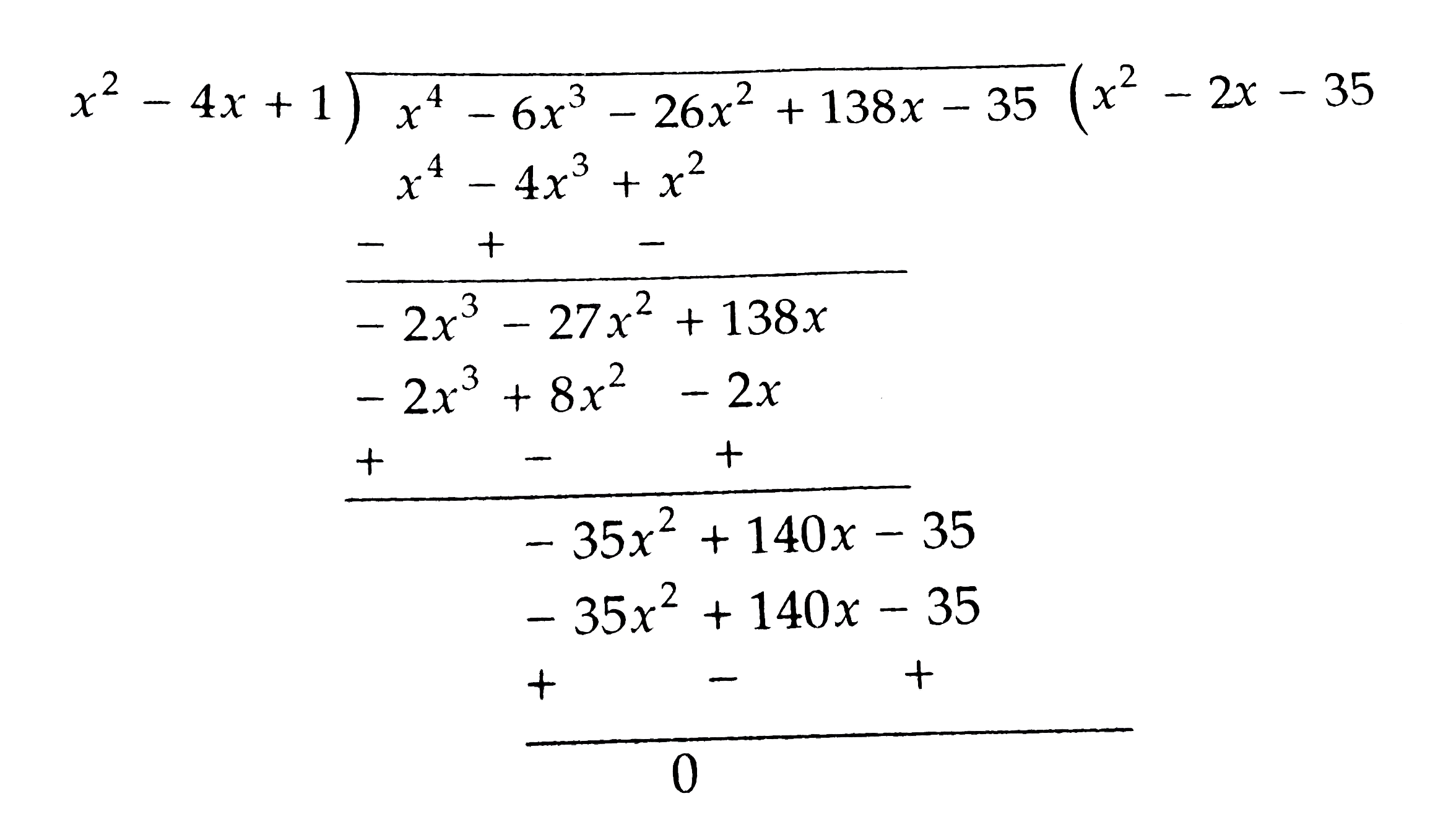
∴f(x)=(x2−4x+1)(x2−2x−35)
अतः बहुपद f(x) के अन्य शून्यक बहुपद x2−2x−35 के शून्यक है |
∵x2−2x−35=x2−7x+5x−35=(x−7)(x+5)
अतः f(x) के अन्य दो शून्यक 7 और -5 है |
Topper's Solved these Questions
- बहुपदBook:RD SHARMAChapter:बहुपदExercise:प्रश्नावली 2.1
Explore 32 Videos
- बहुपदBook:RD SHARMAChapter:बहुपदExercise:प्रश्नावली 2.2
Explore 6 Videos
- प्रायिकताBook:RD SHARMAChapter:प्रायिकताExercise:बहु विकल्पीय प्रश्न
Explore 29 Videos
- रचनाएँBook:RD SHARMAChapter:रचनाएँExercise:प्रश्नावली 11.3
Explore 1 Video
Similar Questions
इन द्विघात बहुपदों के शून्यक ज्ञात कीजिये और शून्यक तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जॉंच कीजिए :
f(x)=x2−2x−8
View Solutionसत्यापित कीजिए कि निम्न त्रिघात बहुपदों के साथ दी गयी संख्याएँ उनकी शून्यक है | प्रत्येक स्थिति में शुन्यकों और गुणांकों के बीच के सम्बन्ध को भी सत्यापित कीजिए :
(i) f(x)=2x3+x2−5x+2,12,1,−2
(ii) g(x)=x3−4x2+5x−2,2,1,1
View Solutionयदि अंको 1, 2,3,4,5,6,7,8,9 में से एक अंक यादृच्छया चुना जाता है, तो एक विषम अंक प्राप्त होने की प्राविकता है:
View Solutionएक 6 सेमी. त्रिज्या वाला वृत्त खींचिए। इसके केन्द्र से 10 सेमी. दूरी पर स्थित एक बिन्दु से वृत्त की स्पर्श रेखाएँ खींचिए तथा उनकी लम्बाई ज्ञात कीजिए।
View SolutionIf two zeroes of the polynomial x4−6x3−26x2+138x−35are 2±√3, find other zeroes.
View Solutionयदि बहुपद x4+x3−11x2−9x+18 के दो शून्यक 1 और -2 है तो इसके अन्य दो शून्यक ज्ञात कीजिए ।
View Solutionबहुपद के शून्यक || उदाहरण
View Solutionदो बहुपदो का लघुतम समापवर्तक x3−6x2+3x+10 है तथा महत्तम समापवर्तक (x+1) है। यदि एक बहुपद x2−4x−5 है तो दूसरा बहुपद ज्ञात कीजिये।
View Solutionबहुपद 2x3+x2−5x+2के अन्य शून्यक ज्ञात कीजिए, यदि इसके दो शून्यक 1 और-2 हैं। ज्ञात कीजिए,
View Solutionद्विघात बहुपद x2+3x−(a+2)(a−1)के शून्यक हैं :,
View Solutionबहुपद के शून्यक
View SolutionIf two zeroes of the polynomial x4−6x3−26x2+138x−35are 2±√3, find other zeroes.
View SolutionRevision|बहुपद#!#बहुपद के शून्यक#!#ज्यामितीय अर्थ
View SolutionIf two zeros of the polynomial f(x)=x4−6x3−26x2+138x−35 are 2±√3 , find other zeros.
View Solutionबहुपद|बहुपदों के प्रकार|बहुपद के शून्यक|बहुपद के शून्यक का जयमितीय अर्थ|अभ्यास कार्य|सारांश
View Solution

