बहुपद $y = a x^{2} + b x + c$ के आलेखों की आकृतियाँ चित्र में दी गयी है :
प्रत्येक आकृति में a, b और c के चिन्ह ज्ञात कीजिये :

Video Solution

Text Solution

Verified by Experts

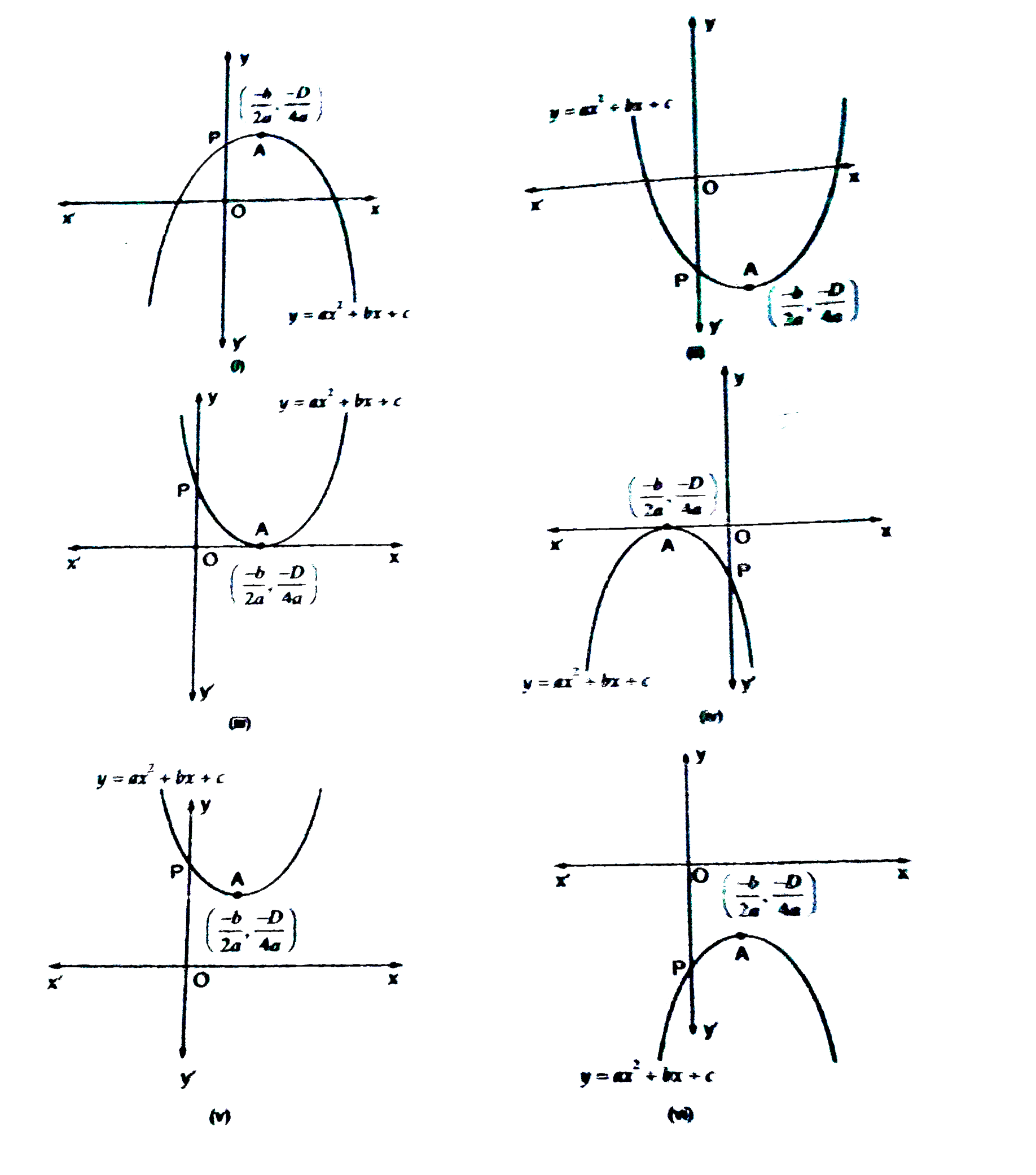
(i) हम निष्कर्ष निकलते है कि $y = a x^{2} + b x + c$ नीचे की ओर खुलने वाला परवलय निरूपित करता है | इसलिए $a < 0$ होगा | हम यह भी प्रेक्षण करते है के परवलय का शीर्ष प्रथम चतुर्थांश (qudrant ) में है |
$∴ - \frac{b}{2 a} > 0 \Rightarrow - b < 0 \Rightarrow b > 0 [∵ a < 0]$
परवलय y = $a x^{2} + b x + c,$ Y - अक्ष को बिंदु P पर प्रतिच्छेद करता है | y - अक्ष पर x = 0 होता है |
$x = 0$ का मान समीकरण $y = a x^{2} + b x + c$ में रखने पर हम y =c प्राप्त करते है |
अतः P के निर्देशांक $(0, c)$ है | चूँकि $P, y$ - अक्ष की धनात्मक दिशा पर स्थित है | अतः $c > 0$
$∴ a < 0, b > 0$ तथा $c > 0$
(ii) दिया है कि $y = a x^{2} + b x + c$ , ऊपर की ओर खुलने वाला परवलय निरूपित करता है | अतः $a > 0$ है | परवलय का शीर्ष चौथे चतुर्थांश में है|
$∴ \frac{- b}{2 a} > 0 \Rightarrow - b > 0 [∵ a > 0]$
परवलय $y = a x^{2} + b x + c, y$ - अक्ष को बिंदु P पर प्रतिच्छेद करता है | $x = 0$ , अतः $y = a x^{2} + b x + c$ में $x = 0$ रखने पर हम $y = c$ प्राप्त करते है |
इसलिए , P के निर्देशांक $(0, c)$ है | चूँकि P, OY' पर स्थित है | अतः $c < 0$
$∴ a > 0, b < 0$ और $c < 0$
(iii) स्पष्टतः $y = a x^{2} + b x + c$ ऊपर की ओर खुलने वाला परवलय निरूपित करता है |
अतः $a > 0$ है |
परवलय का शीर्ष OX पर स्थित है |
$∴ \frac{- b}{2 a} > 0 \Rightarrow - b > 0 \Rightarrow b < 0 [∵ a > 0]$
परवलय $y = a x^{2} + b x + c,$ y - अक्ष को बिंदु P पर प्रतिच्छेद करता है जो OY पर स्थित है | समीकरण $y = a x^{2} + b x + c$ में x = 0 रखने पर, हमे y =c प्राप्त होता है | अतः बिंदु P के निर्देशांक (0, c ) है | चूँकि P, OY अक्ष पर स्थित है |
$∴ c > 0$
$∴ a > 0, b < 0$ और $c > 0$
(iv) परवलय $y = a x^{2} + b x + c$ नीचे की ओर खुलता है | अतः $a < 0$ है |
परवलय का शीर्ष $(\frac{- b}{2 a}, \frac{- D}{4 a})$ , OX' पर स्थित है |
$∴ \frac{- b}{2 a} < 0 \Rightarrow b < 0 [∵ a < 0]$
परवलय $y = a x^{2} + b x + c$ y अक्ष को $P (0, c)$ पर प्रतिच्छेद करता है जो OY' पर है | अतः $c < 0$ है |
$∴ a < 0, b < 0$ तथा $c < 0$
(v) दिया है कि परवलय $y = a x^{2} + b x + c$ ऊपर की ओर खुलता है | अतः $a > 0$
परवलय का शीर्ष $(\frac{- b}{2 a}, \frac{- D}{4 a})$ प्रथम चतुर्थांश में स्थित है |
$∴ \frac{- b}{2 a} > 0 \Rightarrow \frac{b}{2 a} < 0 \Rightarrow b < 0 [∵ a > 0]$
चूँकि $P (0, c), O Y$ पर स्थित है |अतः $c > 0$
$∴ a > 0, b < 0$ और $c > 0$
(vi) स्पष्ट है कि $a < 0$ है | चूँकि $A (\frac{- b}{2 a}, \frac{- D}{4 a})$ चतुर्थ चतुर्थांश में स्थित है |
$∴ \frac{- b}{2 a} > 0 \Rightarrow \frac{b}{2 a} < 0 \Rightarrow b > 0 [∵ a < 0]$
चूँकि $P (0, c), O Y'$ पर स्थित है | अतः $c < 0$
$a < 0, b > 0$ तथा $c < 0$

|

Updated on:21/07/2023

Class 10 MATHS POLYNOMIALS

Topper's Solved these Questions

Similar Questions

RD SHARMA-बहुपद-बहु विकल्पीय प्रश्न

Home
Ask Doubt
Profile