बहुपद $f (x) = x^{2} - 6 x + 9$ का आलेख खींचिये |

Video Solution

Text Solution

Verified by Experts

माना $y = x^{2} - 6 x - 9$
निम्न सारणी x के विभिन्न मानो के लिए y अथवा $f (x)$ के मान दर्शाती है :

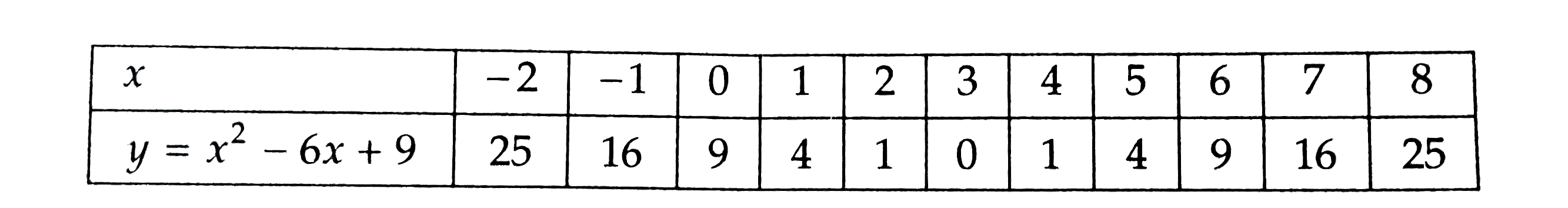
का आलेख बिंदुओं $(- 2, 25), (- 1, 16), (0, 9), (1, 4), (2, 1), (3, 0) (4, 1), (5, 4), (6, 9), (7, 16)$ और $(8, 25)$ से गुजरता है | इन बिंदुओं को आलेख पेपर पर अंकित करके इनसे गुजरने वाला वक्र खींचते है जो के बहुपद $f (x) = x^{2} - 6 x + 9$ का आलेख निरूपित करता है | स्पष्ट है बहुपद का आलेख एक परवलय के रूप में है | हम देखते है कि परवलय का शीर्ष बिंदु $P (3, 0)$ पर है जैसा कि चित्र में दिखाया गया है |

प्रेक्षण : बहुपद $f (x) = x^{2} - 6 x + 9$ के ग्राफ ( आलेख ) से, हम निम्न निष्कर्ष निकलते है :
(i) बहुपद $f (x) = x^{2} - 6 x + 9$ में $x^{2}$ का गुणांक 1 है जोकि एक धनात्मक संख्या है , अतः परवलय ऊपर की ओर खुलता है |
(ii) बहुपद $f (x) = x^{2} - 6 x + 9 = {(x - 3)}^{2}$ के दोनों गुणनखण्ड समान है तथा प्रत्येक $(x - 3)$ के बराबर है | अतः परवलय $y = x^{2} - 6 x + 9, x$ अक्ष को एक बिंदु (3 ,0 ) पर स्पर्श करता है | दूसरे शब्दों में $y = x^{2} - 6 x + 9$ x अक्षो को बिंदु $(3, 0)$ पर स्पर्श करता है | अतः बहुपद के दो समान शून्यक ( zeros ) है |
(iii) बहुपद $f (x) = x^{2} - 6 x + 9$ के दोनों शून्यक 3 के बराबर है | इसलिए परवलय $y = x^{2} - 6 x + 9$ , x - अक्ष को बिंदु $(3, 0)$ पर स्पर्श करता है |
(iv) बहुपद $x^{2} - 6 x + 9$ की $a x^{2} + b x + c$ , से तुलना करने पर, $a = 1, b = - 6$ तथा c = 9 प्राप्त होते है | परवलय का शीर्ष (3, 0 ) अर्थात $(\frac{- b}{2 a}, \frac{- D}{4 a})$ है, जहाँ, $D = b^{2} - 4 a c$ है |
(v) चूँकि $D = b^{2} - 4 a c = 36 - 36 = 0$ है | अतः परवलय x - अक्ष को स्पर्श करता है |

Updated on:21/07/2023

|

Class 10 MATHS POLYNOMIALS

Topper's Solved these Questions

Similar Questions

RD SHARMA-बहुपद-बहु विकल्पीय प्रश्न

Home
Ask Doubt
Profile