यदि किसी △ABC में, △ABC की परित्रिज्या R हो और △ABC का क्षेत्रफल △ है, तो
R=abc4△
R=abc2△
R=abc△
R=4△abc
The correct Answer is:A
Step by step video, text & image solution for यदि किसी triangleABC में, triangleABC की परित्रिज्या R हो और triangleABC का क्षेत्रफल triangle है, तो by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SINE तथा COSINE का सूत्र और उनके अनुप्रयोग Book:KC SINHAChapter:SINE तथा COSINE का सूत्र और उनके अनुप्रयोग Exercise:अभ्यास
Explore 69 Videos
- MODEL TEST PAPER Book:KC SINHAChapter:MODEL TEST PAPER Exercise:वस्तुनिष्ठ प्रश्न
Explore 50 Videos
- अनुक्रम तथा श्रेणी Book:KC SINHAChapter:अनुक्रम तथा श्रेणी Exercise:वस्तुनिष्ठ प्रश्न
Explore 4 Videos
Similar Questions
यदि △ABC के कोण क्रमशः 2:3:7 के अनुपात में हे तो साबित करे कि
a:b:c=√2:2:(√3+1)
View Solutionयदि (If)aN={ax:x∈N}, तो 3N∩7N
View Solutionश्रेढ़ी 1.4+3.7+5.10+.......... के n पदों का योगफल है
View SolutionLet △ABC be a given triangle. If ∣∣∣−−→BA−t−−→BC∣∣∣≥∣∣∣−−→AC∣∣∣ for any t∈R,then △ABC is
View Solution△ABC में tan(A2)=
View SolutionIn △ABC, if acosA=bcosB, then the triangle is
View Solutionयदि △ABC~△PQR एवं BC=3सेमी, QR=4 सेमी और △ABCके क्षेत्रफल =27सेमी2 तो trianglePQR का क्षेत्रफल होगा
View SolutionIn △ABC, if Rr≤2, and a=2, then △ is equal to (△=ar(△ABC)).
View Solution△ABC में मध्यिकाएँ AD , BE और CF बिंदु G से गुजरती है।
यदि GF=4 सेमी हो तो GC का मान ज्ञात कीजिए।
View Solution△ABC में मध्यिकाएँ AD , BE और CF बिंदु G से गुजरती है।
यदि AD=7.5 सेमी हो तो GD का मान ज्ञात कीजिए।
View Solutionएक △ABC में मध्यिकाएँ AD ,BE और CF एक बिंदु G से गुजरती है। यदि AG=6 सेमी , BE=12.6 सेमी और FG=3 सेमी हो , तो AD ,GE और GC ज्ञात कीजिए।
View Solutionएक △ABC की मध्यिकाएँ AD ,BE और CF एक बिंदु G से गुजरती है। यदि AG=5 सेमी ,BE=12 सेमी और FG=3 सेमी हो तो AD ,GE और GC ज्ञात कीजिए।
View Solutionदी गई आकृति में △ABC का बहिर्वृत्त भुजाओ को Q ,P एवं R पर स्पर्श करता है। यदि AQ=8 सेमी हो तो △ABC का परिमाप ज्ञात कीजिए।
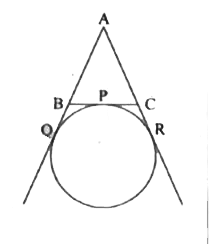
View SolutionLet △ABC be a given triangle. If ∣∣∣−−→BA−t−−→BC∣∣∣≥∣∣∣−−→AC∣∣∣ for any t∈R,then △ABC is
View SolutionIn △ABC if cosA=sinB/sinC then the triangle is
View Solution

