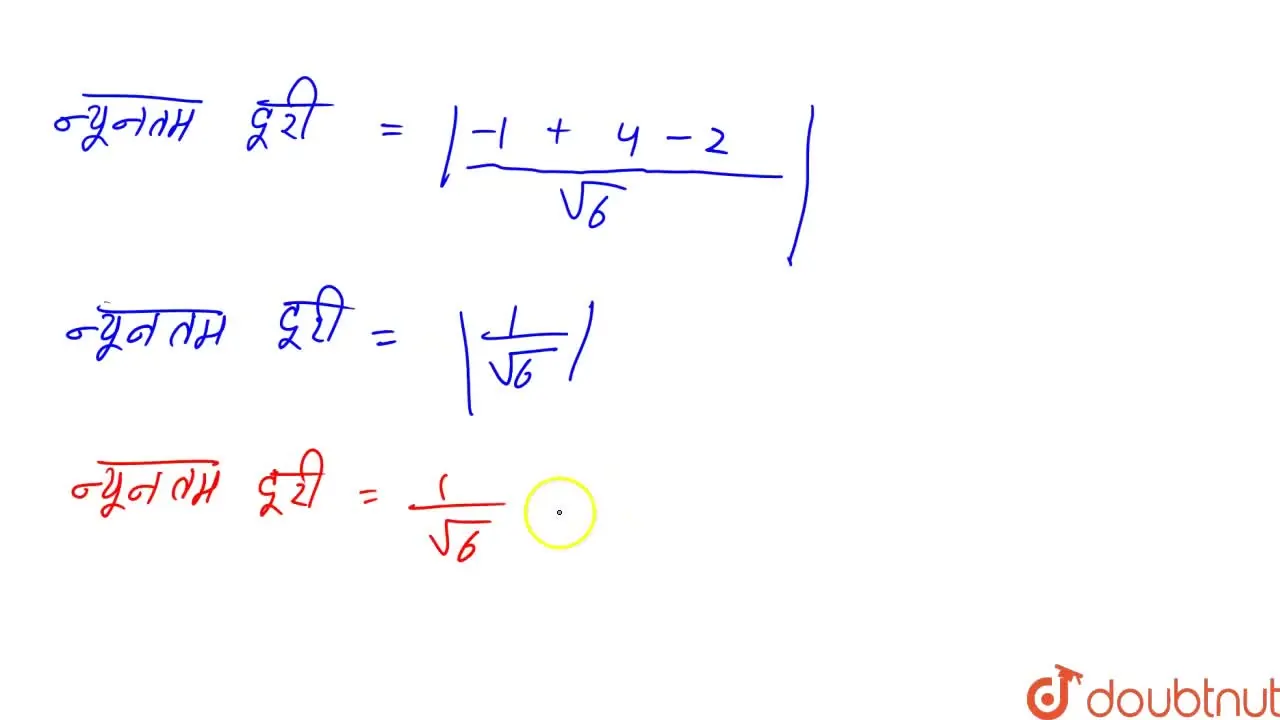दो दिखाएँ जिनके सदिश समीकरण निम्नलिखित हैं, के बीच कि न्यूनतम दुरी ज्ञात कीजिये|
(i) →r=ˆi+2ˆj+3ˆk+λ(2ˆi+3ˆj+4ˆk), तथा (and)
→r=2ˆi+4ˆj+5ˆk+μ(3ˆi+4ˆj+5ˆk)
दो रेखाओं →r=→a1+λ→b1 तथा →r=→a2+μ→b2 के बीच कि न्यूनतम दुरी,
d=∣∣
∣
∣∣(→a2−→a1)(→b1×→b2)∣∣→b1−→b2∣∣∣∣
∣
∣∣............(1)
(i) यहाँ →a1=ˆi+2ˆj+3ˆk,→b1=2ˆi+3ˆj+4ˆk
→a2=2ˆi+4ˆj+5ˆk तथा →b2=3ˆi+4ˆj+5ˆk
अब →a2−→a1=(2ˆi+4ˆj+5ˆk)−(ˆi+2ˆj+3ˆk)
=ˆi+2ˆj+2ˆk.............(2)
→b1×→b2=∣∣
∣
∣∣ˆiˆjˆk234345∣∣
∣
∣∣=(15−16)ˆi−(10−12)ˆj+(8−9)ˆk
=−ˆi+2ˆj−ˆk.........(3)
∣∣→b1×→b2∣∣=√(−1)2+22+(−1)2=√6...........(4)
(→a2−→a1).(→b1×→b2)=(ˆi+2ˆj+2ˆk).(−ˆi+2ˆj−ˆk)
=1×(−1)+2×2+2×(−1)=1........(5)
(4) तथा (5) में प्राप्त मानों को (1) में रखने पर हमें मिलता हैं,
d=∣∣∣1√6∣∣∣=1√6
Related Playlists
Similar Questions
निम्नलिखित प्रत्येक रेखा युग्म के बीच का कोण ज्ञात करें
(i) →r=5ˆi−7ˆj+λ(−ˆi+4ˆj+2ˆk)
→r=−2ˆi+k+μ(3ˆi+4ˆk)
(ii) →r=(2+s)ˆi+(s−1)ˆj+(2−3s)ˆk
→r=(1−t)ˆi+(2t+3)ˆj+ˆk04:43View Solutionमाना कि लड़कों के किसी विघालय के सभी लड़कों का सम्मुच्य A है| दिखाएँ कि सम्मुच्य A पर निम्न प्रकार परिभाषित सम्बन्ध R
(i) R={(a,b):a,b कि बहन है} A में एक रिक्त सम्बन्ध है|
(ii) R′={(a,b):a और b के ऊचाइयों का अंतर 3 मीटर में कम है} A पर एक सार्वत्रिक सम्बन्ध है|05:57View SolutionThe value of f(0), so that the function f(x)=(27−2x)1/3−39−3(243+5x)1/5(x≠0) is continuous at x−0 is given by
06:17View SolutionFind the shortest distance between the two lines whose vector equations are given by: →r=ˆi+2ˆj+3ˆk+λ(2ˆi+3ˆj+4ˆk)and→r=2ˆi+4ˆj+5ˆk+μ(3ˆi+4ˆj+5ˆk)
10:36View Solutionदिखाइए की रेखाएं →r=(ˆi+2ˆj+3ˆk)+λ(2ˆi+3ˆj+4ˆk) तथा →r=(2ˆi+3ˆj+4ˆk)+μ(3ˆi+4ˆj+5ˆk) समतलीय है
(अथवा)
दिखाइए की रेखाएं →r=(ˆi+2ˆj+3ˆk)+λ1(2ˆi+3ˆj+4ˆk) तथा →r=(2ˆi+3ˆj+4ˆk)+λ2(3ˆi+4ˆj+5ˆk) एक-दुसरो को प्रतिच्छेद करती है !05:01View Solutionरेखाओं →r=ˆi+2ˆj+3ˆk+t(2ˆi+3ˆj+4ˆk) तथा →r=2ˆi+4ˆj+5ˆk+s(3ˆi+4ˆj+5ˆk) के मध्य की न्यून्तम दुरी ज्ञात कीजिय |
05:47View Solutionनिम्न रेखाओं के मध्य लघुतम दुरी भी ज्ञात कीजिए जिनके सदिश समीकरण है|
–r=(ˆi+2ˆj+3ˆk)+λ(2ˆi+3ˆj+4ˆk) और –r=(2ˆi+4ˆj+5ˆk)+μ(3ˆi+4ˆj+5ˆk)05:57View SolutionFind the distance between the lines vecr=hati+2hatj-4hatk+lambda(2hati+3hatj+6hatk) and vecr=3hati+3hatj-5hatk+mu(2hati+3hattj+6hatk) .
04:00View SolutionFind the shortest distacne between the lines
→r=ˆi+2ˆj+3ˆk+μ(2ˆi+3ˆj+4ˆk) and →r=(2ˆi+4ˆj+5ˆk)+λ(3ˆi+4ˆj+5ˆk)07:28View Solutionदिखाइए की रेखाएँ →r=(ˆi+2ˆj+3ˆk)+λ1(2ˆi+3ˆj+4ˆj) तथा →r=(2ˆi+3ˆj+4ˆk)+λ2(3ˆi+4ˆj+5ˆk) एक दूसरे को प्रतिच्छेद -बिन्दु भी ज्ञात कीजिए |
04:25View SolutionConsider the lines →r=ˆi+2ˆj+3ˆk+λ(2ˆi+3ˆj+4ˆk) and →r=2ˆi+3ˆj+4ˆk+μ(3ˆi+4ˆj+5ˆk).
i.Convert the equations to cartesian form
ii. Show that the lines are not skew lines.05:19View Solutionनिम्न रेखाओं के मध्य न्यूनतम दूरी ज्ञात कीजिए
→r1=(ˆi+2ˆj+3ˆk)+λ(2ˆi+3ˆj+4ˆk) तथा →r2=(2ˆi+4ˆj+5ˆk)+μ(3ˆi+4ˆj+5ˆk)05:45View SolutionFind the shortest distance between the lines whose equations are : →r=(ˆi+2ˆj+3ˆk)+λ(2ˆi+3ˆj+4ˆk) and →r=(2ˆi+4ˆj+5ˆk)+μ(3ˆi+4ˆj+5ˆk).
06:50View SolutionFind the shortest distance between the lines whose equations are : →r=(ˆi−2ˆj+3ˆk)+λ(ˆi+3ˆj+4ˆk) and →r=(2ˆi+ˆj+5ˆk)+μ(3ˆi−4ˆj−ˆk).
07:12View SolutionFind the shortest distance between the lines given by the. equations : →r=(ˆi+2ˆj+3ˆk)+λ(2ˆi+3ˆj+4ˆk)and →r=(2ˆi+4ˆj+5ˆk)+μ(3ˆi+4ˆj+5ˆk) .
03:14View Solution