यदि −−→AO+−−→OB=−−→BO+−−→OC तो साबित करें कि बिंदुएँ A,B तथा C सरीख हैं|
दिया हैं: −−→AO+−−→OB=−−→BO+−−→OC
⇒−−→AB=−−→BC [सदिशों के योग के त्रिभुज नियम से]
⇒−−→AB∣∣−−→BC
लेकिन −−→AB तथा −−→BC में बिंदु B उभयनिष्ट हैं, इसलिए AB और AC एक ही रेखा हैं|
अतः बिंदुएँ A,B तथा C सरीख हैं|
Topper's Solved these Questions
- सदिश बीजगणित Book:KC SINHAChapter:सदिश बीजगणित Exercise:अभ्यास 25.1
Explore 9 Videos
- सदिश बीजगणित Book:KC SINHAChapter:सदिश बीजगणित Exercise:अभ्यास 25.2
Explore 38 Videos
- वर्धमान और हासमान फलनBook:KC SINHAChapter:वर्धमान और हासमान फलनExercise:अभ्यास 15.1
Explore 47 Videos
- सन्निकटन Book:KC SINHAChapter:सन्निकटन Exercise:Exercise 17.25
Explore 1 Video
Similar Questions
निम्नलिखित मापों को अदिश और सदिश के रूप में वर्गीकरण करें|
(i) 5 सेकंड , (ii) 30km/hr
(iii) 10gm/cm3, (iv) 10 Newton
(v) 20 m/sec towards north, (vi) 1000cm3
View Solutionचार बिंदुओं A,B,C,D के स्थित सिद्ध क्रमश: →a,→b,2→a+3→b तथा →a−2→b हैं| सदिश −−→AC,−−→DB,−−→BC तथा −−→CA को →a और →b के पदों में व्यक्त करें|
View Solutionअन्तराल निकाले जिसमे निम्नलिखित फलन वर्धमान या हासमान है
f(x)=10−6x−2x2
View Solutionएक शंकु की ऊँचाई में वृद्धि 2% है तथा इसका अर्ध शीर्ष कोण अपरिवर्तित है। इसके (i) कुल पृष्ठ क्षेत्रफल (ii) आयतन में
सन्निकट प्रतिशत बढ़ोतरी वृद्धि क्या है?
View SolutionIf →AO+→OB=→BO+→OC , prove that A,B,C are collinear points.
View Solutionif →Ao + →OB = →BO + →OC ,than prove that B is the midpoint of AC.
View SolutionIf →AO+→OB=→BO+→OC , then A,BnadC are (where O is the origin) a. coplanar b. collinear c. non-collinear d. none of these
View SolutionIf | vec AO + vec OB | = | vec BO + vec OC |, then A, B, C form
View SolutionThe magnitudes of vectors vec OA,vec OB and vec OC( in figure( 2-W3) are equal.Find the direction of )/(Ovec A)+vec OB-vec OC.
View SolutionIf −−→AO+−−→OB=−−→BO+−−→OC then A,B,C,D form a/an (A) equilaterla triangle (B) righat angled triangle (C) isosceles triangle (D) straighat line
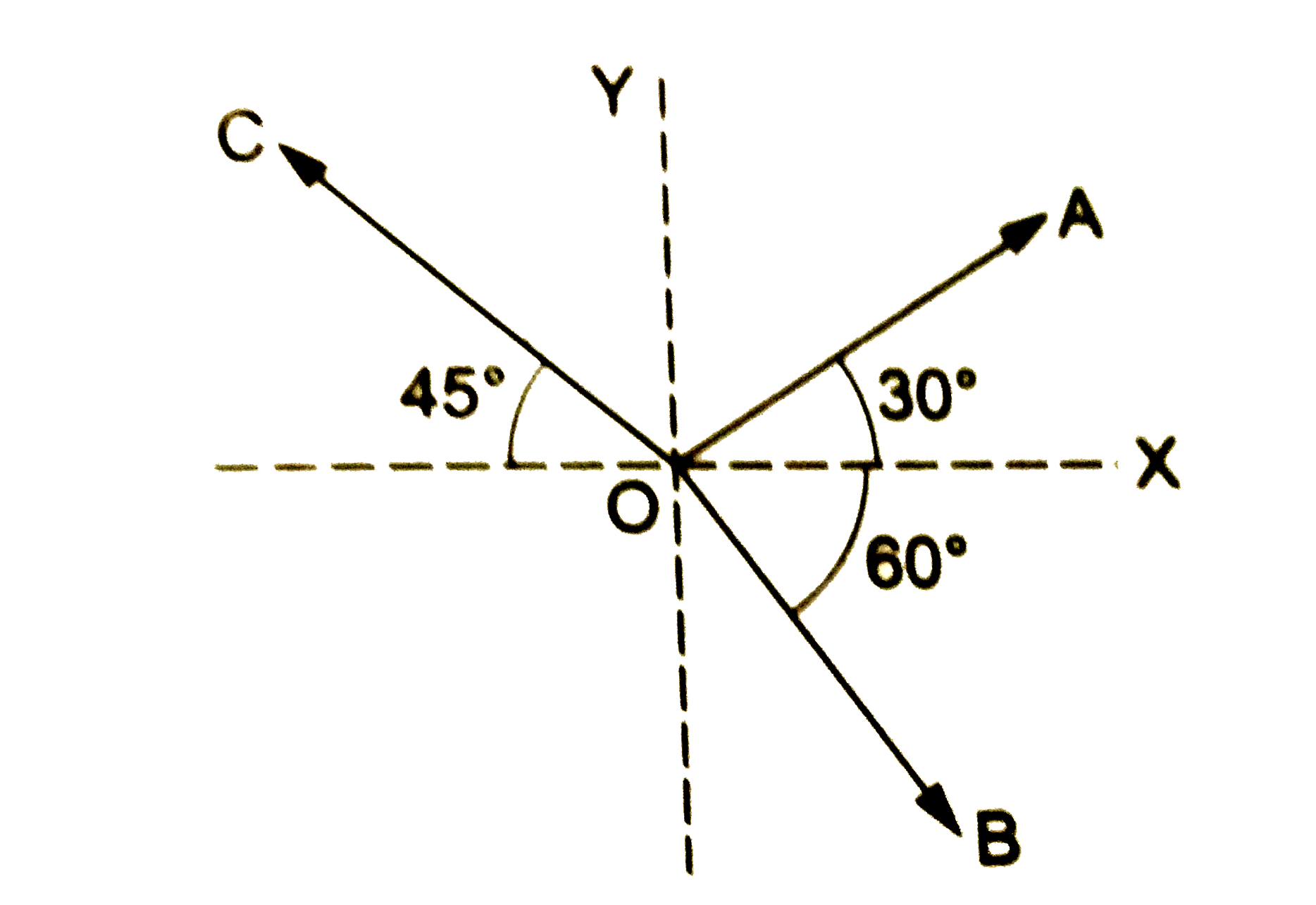
View SolutionThe magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
View Solutionमाना कि O समष्टभुज ABCDEF का केंद्र हैं, तो
−−→OA+−−→OB+−−→OC=−−→OD+−−→OE+−−→OF.
View Solutionदिखाए गए वेक्टरो −−→OA,−−→OB तथा −−→OC के परिमाण बराबर है। वेक्टर −−→OA+−−→OB−−−→OC की दिशा बताएँ।
View SolutionIf OAB is a tetrahedron with edges and ˆp,ˆq,ˆr are unit vectors along bisectors of
−−→OA,−−→OB:−−→OB,−−→OC:−−→OC,−−→OA respectively and ˆa=−−→OA∣∣∣−−→OA∣∣∣,→b=−−→OB∣∣∣−−→OB∣∣∣,→c=−−→OC∣∣∣−−→OC∣∣∣, then :
View Solutionयदि →a,→b,→c समतलीय हो , तो [→a→b→c]=………. होगा।
View Solution

