दीर्घ वृत्त x2a2+y2b2=1 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए ।
दीर्घ वृत्त का समीकरण है,
x2a2+y2b2=1
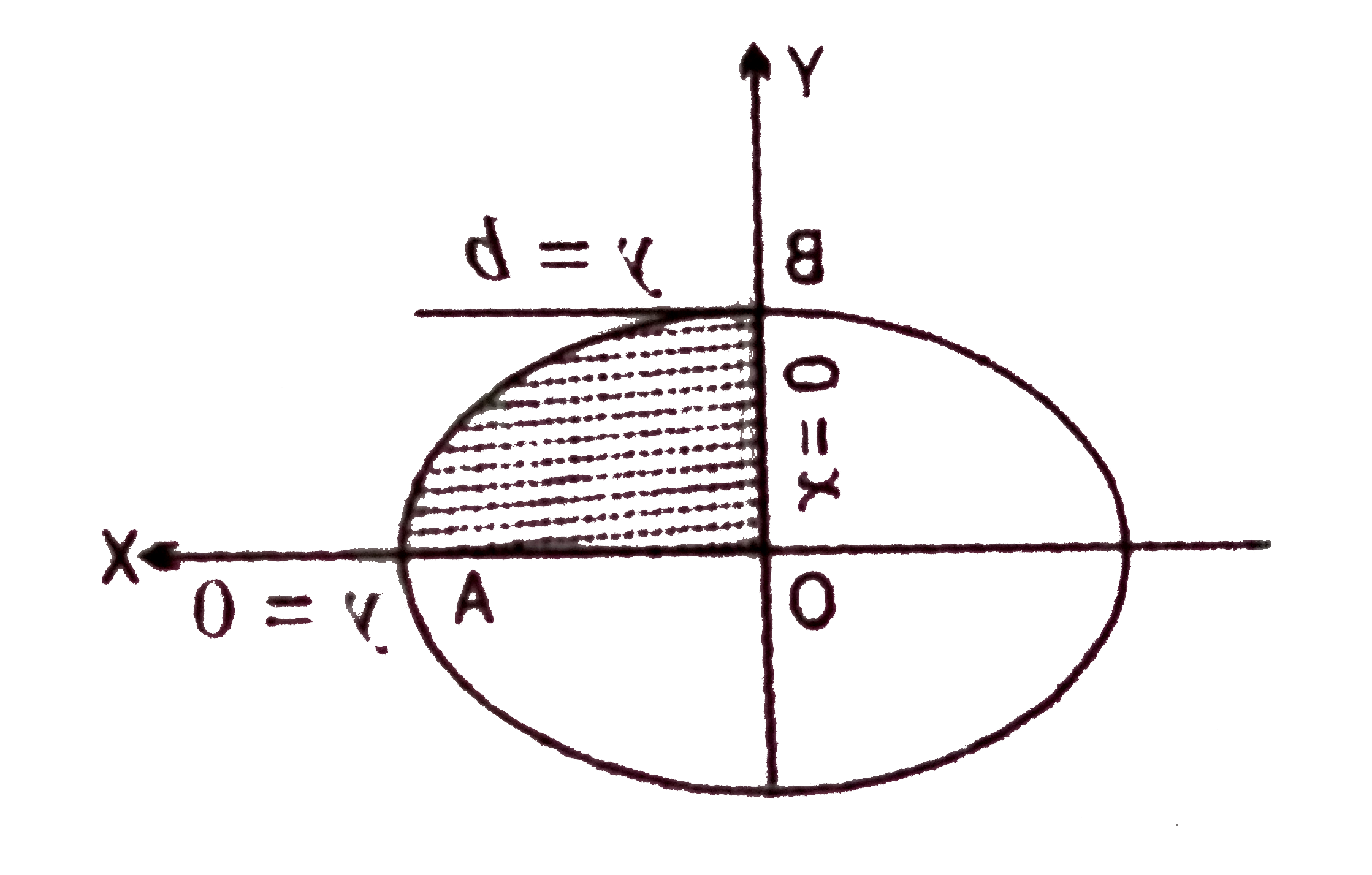
यह x - अक्ष तथा y -अक्ष दोनों के सपक्षे सममित है।
(1) से y=√b2(1−x2a2)=ba√a2−x2 [∵ दीर्घ वृत्त के भाग AB के लिए y≥0]
अब क्षेत्रफल AOBA=∫a0ydx=ba∫a0√a2−x2dx
=ba.πa24 [Ex. (1) से ]
=πab4
∴ दीर्घ वृत्त का क्षेत्रफल =xab वर्ग इकाई
Second method :
क्षेत्रफल AOBA दीर्घ वृत्त, y -अक्ष तथा दो भुजाओं (abscissae ) y = 0 तथा y = b से घिरा है।
∴ क्षेत्रफल AOBA=∫b0|x|dy=∫b0xdy,[∵x≥0]
=∫b0ab√b2−y2dy[∵x2a2+y2b2=1∴x=±ab√b2−y2तथाx≥0]
=ab[y√b2−y22+b22sin−1yb]b0
=ab[0+b22sin−1(1)−(0+0)]
=ab.b22.π2=πab4
∴ दीर्घ वृत्त का क्षेत्रफल =4.πab4 वर्ग इकाई

Topper's Solved these Questions
- वक्र से घिरे क्षेत्र ( समाकलों के अनुप्रयोग )Book:KC SINHAChapter:वक्र से घिरे क्षेत्र ( समाकलों के अनुप्रयोग )Exercise:अभ्यास 22.1
Explore 55 Videos
- वक्र से घिरे क्षेत्र ( समाकलों के अनुप्रयोग )Book:KC SINHAChapter:वक्र से घिरे क्षेत्र ( समाकलों के अनुप्रयोग )Exercise:OBJECTIVE QUESTIONS
Explore 21 Videos
- रोले का प्रमेय एवं लैगरॉंजे का माध्य्मान प्रमेय Book:KC SINHAChapter:रोले का प्रमेय एवं लैगरॉंजे का माध्य्मान प्रमेय Exercise:अभ्यास 13.1
Explore 60 Videos
- वर्ग आव्यूह का सहखण्डज तथा प्रतिलोम Book:KC SINHAChapter:वर्ग आव्यूह का सहखण्डज तथा प्रतिलोम Exercise:अभ्यास
Explore 45 Videos
Similar Questions
वक्र y=x2,रेखाओं y=1,y=2 तथा x− अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए ।
View SolutionThe area bounded by the parabola y2=x, the line y = 4 and the y-axis is
View Solutionफलन f(x)=(x−2)logx पर विचार करते हुए सिद्ध करें की समीकरण xlogx=2−x,1 और 2 के बीच में x कम-से-कम एक मान के लिए अवश्य सत्य है |
View Solutionआव्यूहों के परिवर्त तथा सहखंडज निकाले :
[2351]
View Solutionवक्र y=logx,x−अक्ष,x=1/2तथाx=3/2 से घिरे भाग का क्षेत्रफल ज्ञात कीजिए।
View Solutionवक्रो y=√5−x2तथा y = | x - 1 | से सीमाबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिये |
View Solutionपरवलय y=4−x2 तथा x -अक्ष से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए ।
View Solutionवकों y2=2x+1 तथा x=y+1 से घिरे क्षेत्र का क्षेत्रफल है :
View Solutionदीर्घवृत्त x24+y29=1 से घिरे क्षेत्र का क्षेत्रफल 6π2 वर्ग मात्रक है।
View Solutionसरल रेखा y=2x,X− अक्ष तथा कोटियों x=0 और x=3 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए ।
View Solutionवृत्त x2+y2=a2 तथा वक्र y=|x| से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutionप्रथम चतुर्थांश में रेखाओं x = a, y = a तथा x2+y2=a2 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutionवक्र y=2√x तथा x=0,x=1 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutiony = |x|, x= - 3, x = 1 व x-अक्ष से परिबध्द क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutionवक्रों y2=2x तथा x2+y2=8 के मध्यवर्ती क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutionवक्र y=√4−x2,x=√3y तथा x-अक्ष के मध्य घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solution