मान लीजिए बिंदु A और B पर क्रमशः AP तथा BQ दो ऊर्ध्वाधर स्तम्भ है|यदि ltBrgt AP=16m.BQ=22m AB =20 m हों तो AB पर एक ऐसा बिंदु R ज्ञात कीजिए ताकि RP2+RQ2 निम्नतम हो|
माना की AR =x मीटर
दिया है AP=16m,BQ=22m=AB=20m
(##KCSHINMATXIIP1C18SLV034_S01.png width=80%><br> therefore RB =(20 -x)m<br>मानाकी y= RP^(2)+RQ^(2) तो<br> y= (x^(2) +16^(2))+(20-x)^(2) +22^(2)<br> = x^(2) +(20-x)^(2) +16^(2) +22^(2...(1)<br>ttherefore " "(dy)/(dx) =2x -2 (20-x) =2 (x-20+x)<br>= 2(2x-20 ) =4 (x-10)" "...(2)<br>yकेमहत्तमयान्यूनतममानकेलिए (dy)/(dx) =0<br> therefore 4(x-10) =0rArr x=10 <br>(2)से, (d^(2)y)/(dx^(2))=4gt 0<br>अतःyन्यूनतम(यहाँनिरपेक्षन्यूनतमहोगाजबx=10<br>अतः RP^(2) +RQ^(2) केन्यूनतममानकेलिए AR =x=10m
Topper's Solved these Questions
- उच्चतम और निम्नतम BOOK - KC SINHACHAPTER - उच्चतम और निम्नतम EXERCISE - प्रश्नावली 18.1
69 Videos
- आव्यूहBOOK - KC SINHACHAPTER - आव्यूहEXERCISE - OBJECTIVE QUESTIONS
23 Videos
- त्रिविमीय ज्यामिति दो रेखाओ के बीच का कोण BOOK - KC SINHACHAPTER - त्रिविमीय ज्यामिति दो रेखाओ के बीच का कोण EXERCISE - अभ्यास 28.1
18 Videos
Similar Questions
निम्नलिखित फलन के सभी स्थानीय उच्चतम मान और न्यूनतम बिंदुओं , यदि कोई हो तो ज्ञात कीजिए तथा संगत उच्चतम और निम्नतम मान भी ज्ञात कीजिए| f(x)=x3−6x2+9x+15
View SolutionX और y के दिए गए मानों में से कौन-सा जोड़ा निम्न जोड़े को समान बनाता है [3x+75y+12−3x][0y−28 4]
View Solutionयदि एक रेखा x ,y तथा z -अक्ष कि धनात्मक दिशा के साथ क्रमशः 90∘,60∘,30∘ का कोण बनती है तो इसकी दिक्-कोसाइन ज्ञात कीजिए.
View SolutionLet AP and BQ be two vertical poles at points A and B respectively. If AP=16m, BQ=22m and AB=20m , then find the distance of a point R on AB from the point A such that RP2+RQ2 is minimum.
View Solutionमान लीजिए बिंदु A और B पर क्रमशः AP तथा BQ दो उर्ध्वाधर स्तंभ है| यदि AP = 16 m, BQ = 22 m और AB = 20 m हों तो AB पर एक ऐसा बिंदु R ज्ञात कीजिए ताकि RP2+RQ2 निम्नतम है |
View Solutionमान लीजिए बिंदु A और B पर क्रमशः AP तथा BQ दो ऊध्वर्रधकर स्तम्भ है । यदि AP =16 मि, BQ =22 मि और AB = 20 मि हो तो AB पर एक ऐसा बिंदु R ज्ञात कीजिए ताकि RP2+RQ2 निम्नतम हो।
View Solutionरेखाखण्ड AB अक्षो के बीच इस प्रकर गति करता है की A सदैव Y-अक्ष पर तथा B सदैव X- अक्ष पर हो । रेखाखण्ड AB पर एक बिंदु P इस प्रकार है की PA =a और PB =b यदि AB=a+b हो , तो बिंदु P का बिन्दुपथ ज्ञात कीजिये
View Solutionबिंदु P,Q,R,S के निर्देशांक (2,a),(3,5),(3,4)और (0,6) है । यदि रेखा PR लंबवत हो QS पर तो a का मान ज्ञात कीजिए ।
View Solutionबिंदु P(a,b) सरल रेखा 3x+2y=13 पर तथा बिंदु Q(b,a)सरल रेखा 4x−y=5 पर स्थित है तो रेखा PQ का समीकरण ज्ञात कीजिए।
View Solutionदो स्थिर बिंदु A और B के निर्देशांक क्रमशः (a,0) और (−a,0) है , तो चर बिंदु P का बिन्दुपथ ज्ञात कीजिए जबकि :
PA=nPB , जहाँ n अचर है ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
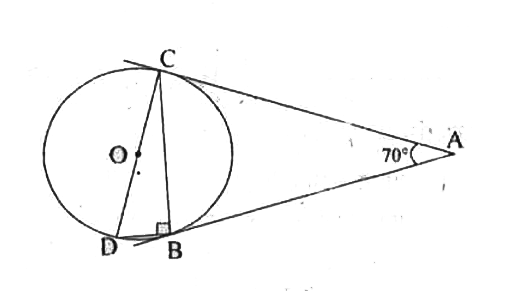
View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।

View Solutionयदि ¯¯¯¯¯¯OA=¯a,¯¯¯¯¯¯OB=¯b तथा C,AB पर एक ऐसा बिंदु है कि ¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB तो सदिश ¯¯¯¯¯¯OC बराबर है:
View Solutionयदि बिंदु A(a,0) और B(−a,0) दो स्थिर बिंदु हों तो उस बिंदु का बिन्दुपथ ज्ञात कीजिए जिस पर रेखाखण्ड AB सदैव समकोण बनाता है ।
View Solutionएक छड़ की लम्बाई l है । इसका एक सिरा भूमि पर तथा दूसरा सिरा एक ऊर्ध्वाधर दीवार पर टिका है । यदि छड़ भूमि पर फिसले , तो उसके मध्य बिंदु का बिन्दुपथ ज्ञात कीजिए ।
View Solution
