अन्तराल निकाले जिसमे फलन
$f (x) = \frac{x}{1 + x^{2}}$
$(a)$ वर्धमान है $(b)$ हासमान है

A

$(a) (- 1, 1)$
$(b) (- \infty, - 1)$

B

$(a) (- 1, 1)$
$(b) (1, \infty)$

C

$(a) (- 1, 1)$
$(b) (- \infty, - 1) \cup (1, \infty)$

D

$(a) (- 1, 0)$
$(b) (- \infty, - 1) \cup (1, \infty)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

यहाँ $f (x) = \frac{x}{1 + x^{2}}$
$\Rightarrow f' (x) = \frac{(1 + x^{2}) \cdot 1 - x \cdot 2 x}{{(1 + x^{2})}^{2}} = \frac{1 - x^{2}}{{(1 + x^{2})}^{2}} = \frac{(1 - x) (1 + x)}{{(1 + x^{2})}^{2}}$
चूकि ${(1 + x^{2})}^{2} > 0$ , इसलिए $f' (x)$ का चिह योजना $(1 - x) (1 + x)$ के लिए चिह योजना के सामान होना।
$f' (x)$ अर्थात $(1 - x) (1 + x)$ कि चिह योजना

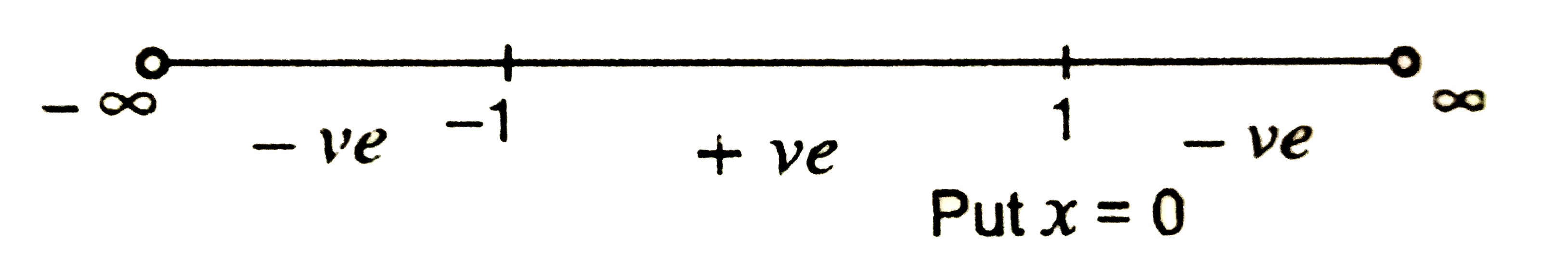
$f' (x)$ कि चिह योजना से स्पष्ट है कि
$(i)$ अंतराल $(- 1, 1)$ तथा $[- 1, 1]$ में भी f $न ि र ं त र व र ् ध म ा न ह ै । < b r > क ् य ो क ि$ f $,$ x=-1 $त थ ा$ x=1 $प र स ं त त ह ै । < b r >$ (ii) f $,$ (-oo,-1) $त थ ा$ (1,oo) $म े ं ह ा स म ा न फ ल न ह ै त थ ा य ह$ (-oo,1] $त थ ा$ [1,oo)में भी हासमान फलन है।

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

KC SINHA-वर्धमान और हासमान फलन-अभ्यास 15.1

Home
Ask Doubt
Profile