Q पर निम्न प्रकार से परिभाषित द्विआधारी संक्रिया ∗ के क्रमविनिमेय तथा साहचर्य होने की जाँच करें।
a∗b=a−b+ab सभी a,b∈Q के लिए
यहाँ a∗b=a−b+ab सभी a,b∈Q के लिए।
क्रमविनिमेय: सभी a,b∈Q के लिए,
a∗b=a−b+ab तथा b∗a=b−a+ba
चूँकि a−b+ab≠b−a+ba कुछ a,b∈Q के लिए [ हम a=1,b=2 ले सकते है ]
∴a∗b≠b∗a
अतः ∗, समुच्चय पर क्रमविनिमेय नहीं है।
साहचर्य : माना कि a,b,c∈Q.
तो a∗(b∗c)=a∗(b−c+bc)
=a−(b−c+bc)+a(b−c+bc)
=a−b+c−bc+ab−ac+abc ...(1)
तथा (a∗b)∗c=(a−b+ab)c
=(a−b+ab)−c+(a−b+ab)c
=a−b+ab−c+ac−bc+ab
=a−b−c+ab+ac−bc+abc ...(2)
(1 ) से (2 ) से,
a∗(b∗c)≠(a∗b)∗c कुछ a,b,c∈Q के लिए [a=0,b=1,c=2 के लिए]
अतः ∗, समुच्चय Q पर साहचर्य है।
Topper's Solved these Questions
- द्विचर संक्रिया BOOK - KC SINHACHAPTER - द्विचर संक्रिया EXERCISE - अभ्यास 3.1
64 Videos
- दो सदिशों का सदिश या क्रॉस गुणनफल BOOK - KC SINHACHAPTER - दो सदिशों का सदिश या क्रॉस गुणनफल EXERCISE - अभ्यास 27.2
11 Videos
- द्वितीय कोटि का अवकलज BOOK - KC SINHACHAPTER - द्वितीय कोटि का अवकलज EXERCISE - OBJECTIVE QUESTIONS
5 Videos
Similar Questions
यदि Z+ सभी अऋणात्मक पूर्णांकों का समुच्चय है तो निर्धारित कीजिए कि क्या निम्नलिखित प्रकार से परिभाषित संक्रिया ∗ से एक द्विआधारी संक्रिया प्राप्त होती है या नहीं। उस दशा में जब ∗ एक द्विआधारी संक्रिया नहीं है, औचित्य भी बतलाइए।
Z+ पर a∗b=a−b+5 द्वारा परिभाषित संक्रिया ∗
View Solutionदिखाएँ कि तीन बिन्दुएँ जिनके सदिश −3ˆi+ˆj+5ˆk,2ˆi+3ˆk,−13ˆi+3ˆj+9ˆk हैं, संरेख हैं |
View SolutionIf x=a(cosθ+θsinθ),y=a(sinθ−θcosθ), then d2ydx2=
View Solutionअभिक्रिया 12A→2B के लिए 'A' के विघटन की दर B' के बनने की दर से निम्न प्रकार सम्बंधित है
View Solutionअऋण (Non - negative ) संख्याओं के समुच्चय W पर संक्रियां * निम्न प्रकार परिभाषित है a ∗b=a^(b) सिद्ध कीजिए की * समुच्चय W पर द्विआधारी संक्रिया नहीं है|
View SolutionZ में a∗b =a-bद्वारा परिभाषित द्विआधारी संक्रिया*के लिए निर्धारित कीजिए कि क्या*द्विआधारी, क्रमविनिमेय तथा साहचर्य है ?
View Solutionएक द्विआधारी संक्रिया ∗Z+ पर निम्न रूप परिभाषित है :
a∗b=ab−bजहाँa,b∈Z+
2∗5 का मान ज्ञात कीजिए , जहाँ Z+ धनात्मक पूर्णांकों का समुच्चय है ।
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionयदि संक्रिया ∗ वास्तविक संख्याओं के समुच्चय R पर द्विआधारी संक्रिया है तथा इस प्रकार परिभाषित है कि
a∗b=√a4+b4 , जहाँ a,b∈R से दिखाइए कि '∗' क्रम-विनिमेय नियम का पालन करती है।
View Solutionयदि द्विआधारी संक्रिया ∗ वास्तविक संख्याओं के समुच्चय R पर इस प्रकार परिभाषित है कि
a∗b=ab2+1, जहाँ a,b∈R
तो द्विआधारी संक्रिया ∗ के साहचर्यता (associativity) की जाँच कीजिए।
View Solutionअभिक्रिया (A+B)→उत्पाद के लिये निम्न आँकड़े प्राप्त हुए |
इन आँकड़ों से A एवं B के सन्दर्भ में अभिक्रिया की कोटि तथा सम्पूर्ण अभिक्रिया की कोटि का निर्धारण कीजिए।
View Solutionफलनों के प्रकार पर आधारित प्रश्न|द्विआधारी संक्रियाएँ
View SolutionRevision |Exam Special #!#पूर्णांकों के गुणन के लिए साहचर्य गुण तथा वितरण गुण
View Solutionकार्य तथा कार्य के प्रकार#!#ऊर्जा तथा ऊर्जा के प्रकार
View Solutionपदार्थ A और B के बीच अभिक्रिया को निम्न प्रकार दर्शाया गया है
A+B−→C इस अभिक्रिया की दर से निम्न प्रेक्षणों को प्राप्त किया जाता है

View Solutionनिम्न के लिए हाइड्रोजनीकरण की ऊष्मा की तुलना कीजिए-
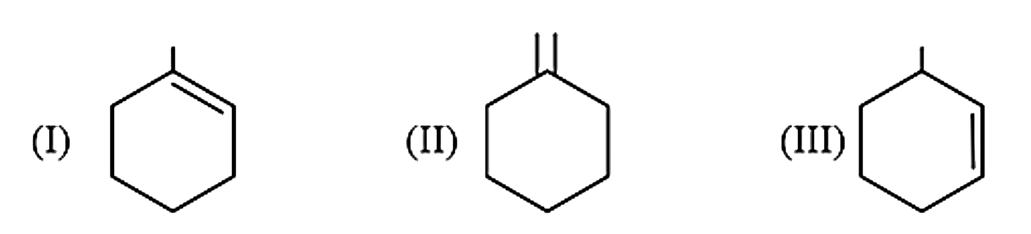
View Solution
