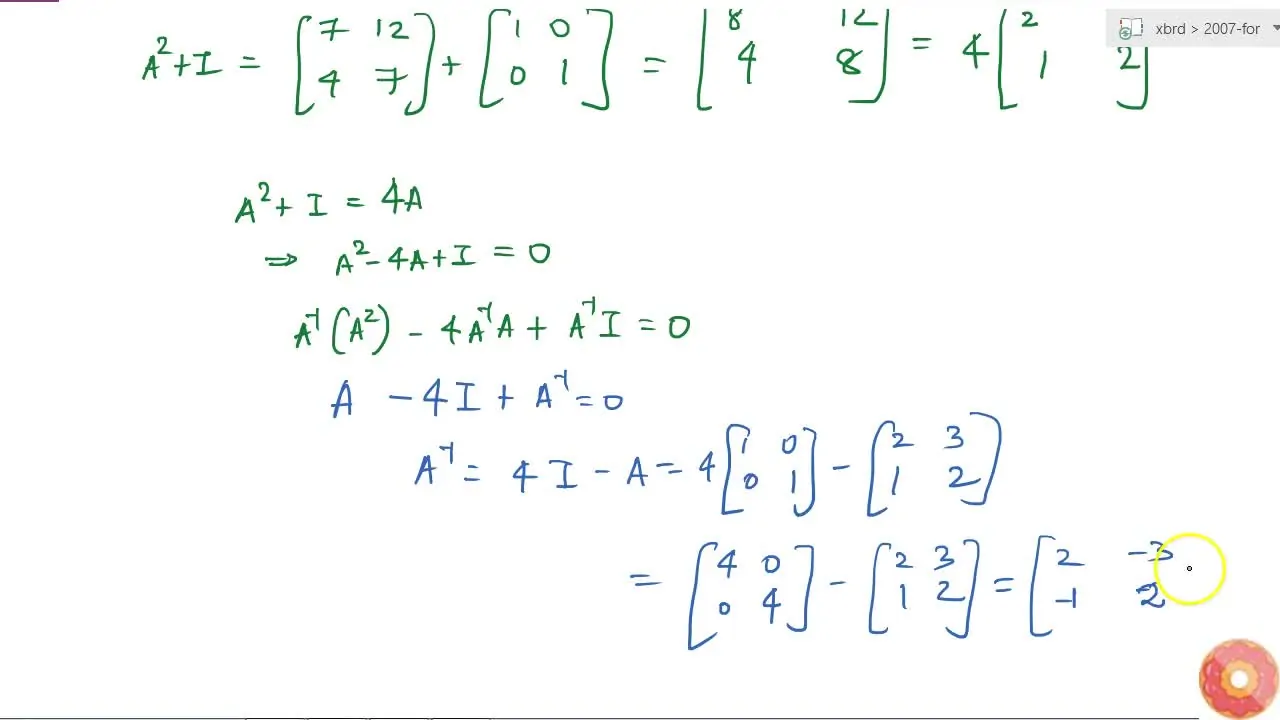For the matrix A=[2312] show that A2−4A+I=0 Hence find A−1
Video Solution
|
Answer
Step by step video & image solution for For the matrix A=[(2,3),(1,2)] show that A^2-4A+I=0 Hence find A^-1 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Related Playlists
Similar Questions
For the matrix A=[2312] show that A2−4A+I=0 Hence find A−1
View SolutionIf A=[53127], show that A2−12A−I=0. Hence find A−1.
View SolutionIf A=[3112], show that A2−5A+5I=0. Hence, find A−1.
View SolutionFor the matrix, A=[1−123] show that A2−4A+5I=0 and also find A−1
View SolutionIf A=[31−12], show that A2−5A+7I=O. Hence, find A−1.
View SolutionIf A=[2−334], show the A2−6A+17I=0. Hence find A−1
View SolutionIf A=⎡⎢⎣2−11−12−11−12⎤⎥⎦ show that A2−5A+4I=0
Hence find A−1View SolutionIf A=[31−12] then show that A2−5A+7I=0 Hence find A−1
View SolutionFor the matrix A=[3211] Find a & b so that A2+aA+bI=0. Hence find A−1
View SolutionIf A=[42−11], show that (A-2 I) A-3 I) =0
View Solution