Show that all harmonics are present on a stretched string between two rigid supports.
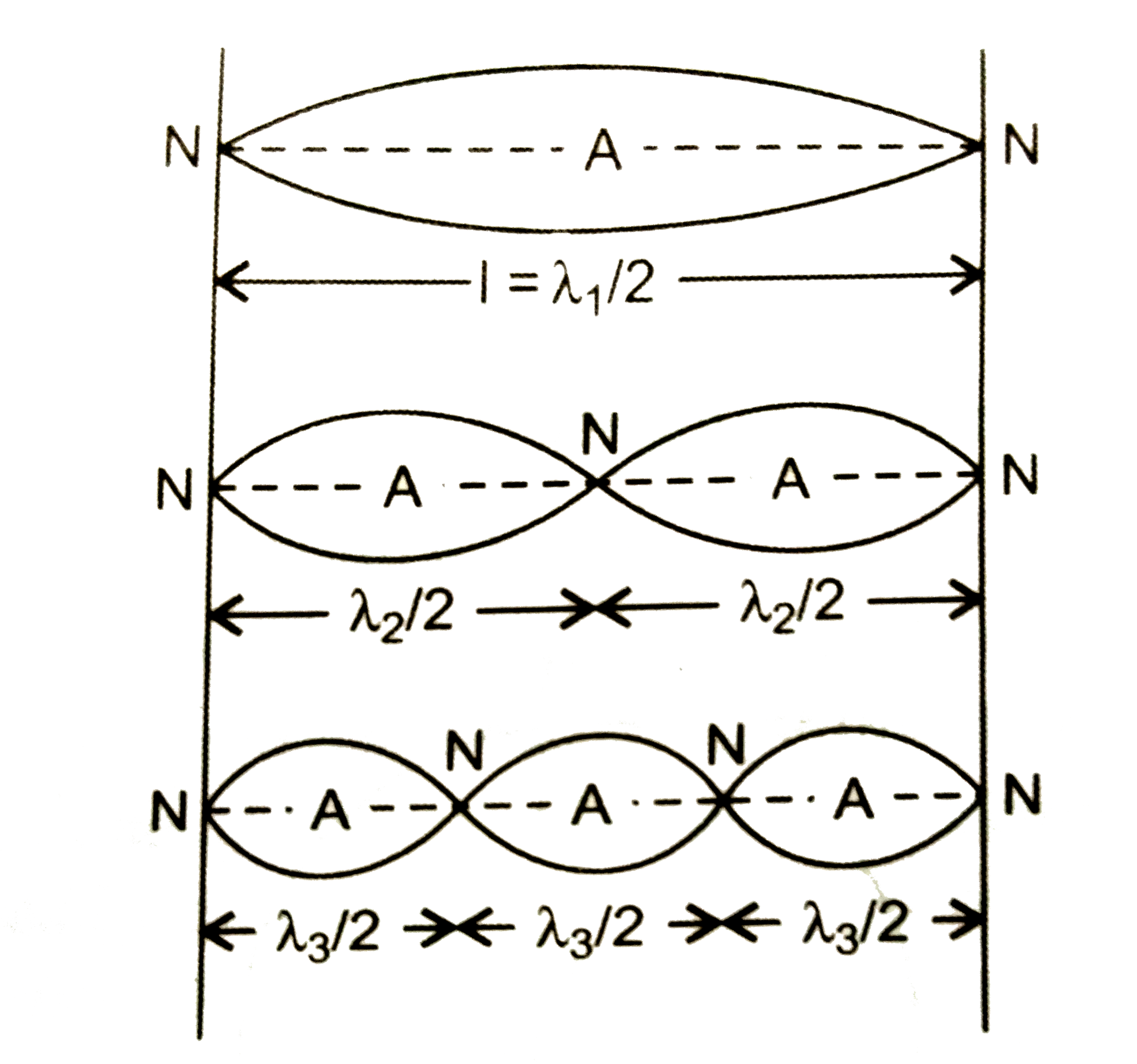
Consider a string of length l, stretched under tension T between two fixed points. If the string is plucked and then released, transverse harmonic wave propagates along its length and is reflected at the end.
Frequency of vibrations is given by n=1λ√Tm
For obtaining P loops in string , it has to be plucked at a distance l/2P from one fixed end.
For first mode of vibration:
λ1=2l
l=λ12
If n1 be the frequency of vibration of the string and v the speed of wave in the string
n1=vλ1=v2l
n1=12l×√Tm..........(i)
This is the fundamental frequency for first harmonic. For second mode of vibrations:
λ2=2l2
∴n2=22l×√Tm
n2=2n1 [from equation (i)]
For third mode of vibrations :
λ3=2l3
n3=32l×√Tm=3n1 [from equation (i)]
In general, if the string is plucked at length l/2P, then it vibrates in P segments (loops) and we have Pth harmonic
nP=P2l√Tm
Thus, the frequencies of the fundamental tone and the overtones of a stretched string have the following relationship :
n1:n2:n3..........,nP=1:2:3......:p
These frequencies are in harmonic series with both even and odd harmonics.
Topper's Solved these Questions
- OCTOBER 2015BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - OCTOBER 2015EXERCISE - SECTION-2
21 Videos
- OCTOBER 2015BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - OCTOBER 2015EXERCISE - SECTION-2
21 Videos
- MARCH 2017BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2017EXERCISE - SECTION II
21 Videos
- SEPTEMBER 2014BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - SEPTEMBER 2014EXERCISE - SECTION-2
21 Videos
Similar Questions
Show that all harmonics are present on a stretched string between two rigid supports.
View SolutionTwo strings of same material are joined to form a large string and is stretched between rigid supports. The diameter of the second string is twice that of the first. It was observed in an experiment that the whole string was oscillating in 4 loops with a node at the joint. Find the possible lengths of the second string if the length of first string is 90 cm.
View Solution
Knowledge Check
Show that all harmonics are present on a stretched string between two rigid supports.
Aa nodeBan antinodeCeither a node or an antinodeDneither a node nor an antinode.A second harmonic has to be generated in a string of length l stretched between two rigid supports. The point where the string has to be plucked and touched are
APlucked at l/4 and touch at l/2BPlucked at l/4 and touch at 3l/4CPlucked at l/2 and touched at l/4DPlucked at l/2 and touched at 3l/4A wire having a linear density of 0.05 kg/m is stretched between two rigid supports. The tension in the wire is 4.5×107 dyne . If the observed that the wire resonates at a frequency of 420 Hz and the next higher frequency at which the wire resonates is 490 Hz, then the length of the wire would be
A75 cmB21.4 cmC214mD114m
In Fig. 16-13, two strings have been tied together with a knot and then stretched between two rigid supports. The strings have linear densities μ1=1.4×10−4 kg/m andμ2=2.8.×10−4kg/m. Their lengths are L1=3.0mandL2=2.0m, and string 1 is under a tension of 400 N. Simultaneously, on each string a pulse is sent from the rigid support end, toward the knot. Which pulse reaches the knot first.

Figure 18-13 Two strings, of lengths L1andL2, tied together with a knot and stretched between two rigid supports.
View SolutionA wire having a linear density of 0.05gm/c is stretched between two rigid supports with a tension supports with a tension of 4.5×107 dynes. It is oberserved that the wire resonates at a frequency of 420cycles/sec. the next higher frequency at which the same wire resonates is 490cycles/sec. Find the possible mode of vibration of string initially :
View SolutionA wire having a linear density of 0.05gm/c is stretched between two rigid supports with a tension supports with a tension of 4.5×107 dynes. It is oberserved that the wire resonates at a frequency of 420cycles/sec. the next higher frequency at which the same wire resonates is 490cycles/sec. Find the possible mode of vibration of string initially :
View SolutionA second harmonic has to be generated in a string of length l stretched between two rigid supports. The point where the string has to be plucked and touched are
View SolutionA wire having a linear density of 10−3 kg/m is stretched between two rigid supports. The tension in the wire is 25.6N . If the observed that the wire resonates at a frequency of 480 Hz and the next harmonic is found to be 640 Hz, then the length of the wire will be
View Solution
