Obtain an expression for potential energy of a particle performing simple harmonic motion. Hence evaluate the potenhtial energy (a) at mean position and (b) extreme position.
A horizontal disc is freely rotating about a transverse axit passing through its centre at the rate of 100 revolutions per minute. A 20 gram blob of wax falls on the disc and sticks to teh disc at a distance of 5 cm form its axis. Moment of inertia of the disc about its axit passing through its centre of mass is $2 \times 10^{- 4}$ kg $m^{2}$ . Calculate the new frequency of rotation of the disc.

Video Solution

Text Solution

Verified by Experts

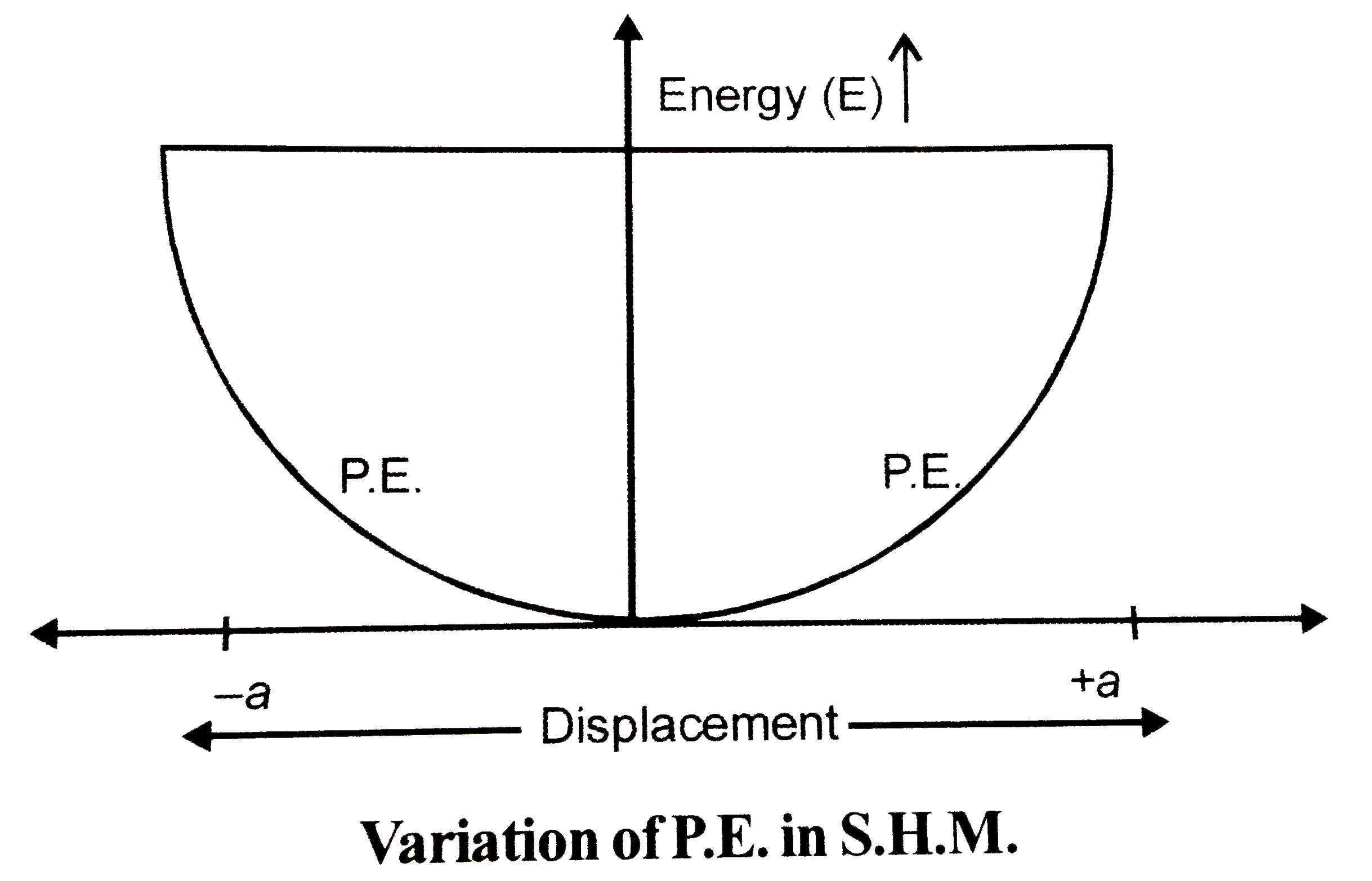
An osciliating particle possesses both types of energies potential as well sa kinetic. It possesse potential energy position.
Ptential energy : Condsider a particle of mass m executing S.H.M. Let x be its displacement from F acting upon the particle is proportinal to ans opposite to the displacement x, we have
$F = - k x$
Where, the constant k gives the force per unit displacement, the for can also be expressed in terms of potential energy U of the particle is proportionla to and opposite to the displacement x, we have
$F = - k x$
Where, the constant k gives the force per unit displacemenjt. The force can also be expressed in terms of potential energy U of the particle as :
$F = - \frac{d U}{d x}$
$thus, \frac{d U}{d x} = k x$
On integrating, we get
$U = \frac{1}{2} {kx}^{2} + C$
Where C is a constant. If we assume the ppotential energy zero in the equilibrium position, i.e., ,
If $U = 0$ at $x = 0,$ then $C = 0$ .
Therefore, $U = \frac{1}{2} {kx}^{2}$
Potential energy, $U = \frac{1}{2} m ω^{2} x^{2} [∵ k = m ω^{2}]$
Hence for above it is clear that the potential energy of a particle performing S.H.M. is maximum and displacement is minimum i.r., x = 0 .
$P.E. = \frac{1}{2} m ω^{2} x^{2} = 0$
(b) Potential energy at extreme position : At extreme position, velocity of a particle executing S.H.M. is munumum and displacement is maximum, e.i., $x = \equiv a$
$P.E. = \frac{1}{2} m ω^{2} x^{2} = 0$

Given : $n_{1} = 100 r.p.m.$
$= \frac{100}{60} = 1 \cdot 66 r . p . s .$
$m = 20 gm$
$h = r = 5 c m = 0 \cdot 05 m$
$I_{1}$ = Moment of inertia of the disc about its axiws $= 2 \times 10^{- 4} {kgm}^{2}$ .
$I_{2}$ = Moment of inertia of the disc about same axis with To wax.
To find: $n_{2} = ?$
From formula,
$I_{2} = I_{1} + m r^{2} [Formparallel axis theorem ]$
$I_{1} ω_{1} = I_{2} ω_{2}$
$I_{1} (2 π n_{1}) = (I_{1} + m r^{2}) (2 π n_{2})$
$I_{1} n_{1} = (I_{1} + m r^{2}) n_{2}$
$n_{2} = \frac{I_{1} n_{1}}{I_{1} + {mr}^{2}}$
$n_{2} = \frac{2 \times 10^{- 4} \times 166}{2 \times 10^{- 4} + (2 \times 10^{- 2} \times 0.05 \times 0.05)}$
$= \frac{2 \times 10^{- 4} \times 1 \cdot 66}{2 \times 10^{- 4} + 0.5 \times 10^{- 4}}$
$= \frac{2 \times 10^{- 4} \times 1 \cdot 66}{2.5 \times 10^{- 4}}$
1*328"r.p.s"

Updated on:21/07/2023

The velocity of a particle performing simple harmonic motion, when it passes through its mean position i
AInfinity
BZero
CMinimum
DMaximum
The time period of a particle in simple harmonic motion is T. Assume potential energy at mean position to be zero. After a time of $\frac{T}{6}$ it passes its mean position its,
Avelocity will be half its maximum velocity
Bdisplacement will be half its amplitude
Cacceleration will be nearly $86 %$ of its maximum
D $K E = P E$
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increased
Bchanges if its axis of rotation is changed
Cincreases if its angular velocity is increased
Dboth (a) and (b) are correct