If $α, β, γ$ are direction angles of a line l, then prove that
${cos}^{2} α + {cos}^{2} β + {cos}^{2} γ = 1$ .
Hence, deduce that ${sin}^{2} α + {sin}^{2} β + {sin}^{2} γ = 2$ .

Video Solution

Text Solution

Verified by Experts

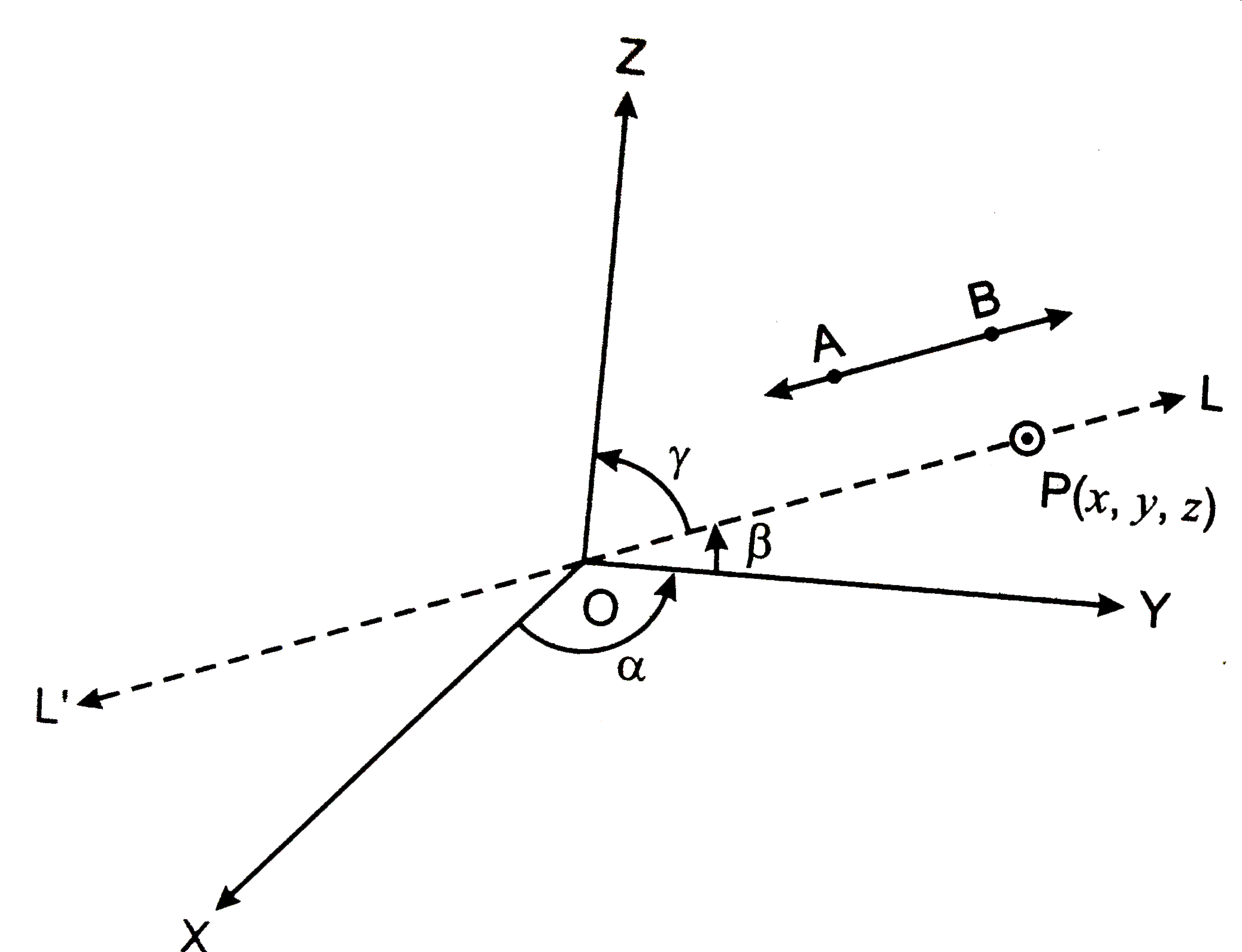
Consider line L passing through origin and parallel to the line AB.
Let P (x, y, z )be a point on L and l (OP)=r.
Position vectro of point P is
$- - \to O P = x ˆ i + y ˆ j + z ˆ k ... ... (A)$
If $α, β & γ$ are the direction angles and l, m, n, are direction cosines of line OP.
Then $l = cos α, m = cos β, n = cos x$
Consider $- - \to O P . ˆ i = (x ˆ i + y ˆ j + z ˆ k . ˆ i = x ... ... . (i)$
Also $- - \to O P ˆ i = ∣ ∣ ∣ - - \to O P ∣ ∣ ∣ ∣ ∣ ˆ i ∣ ∣ . cos α = r cos α ... ... (i i)$
From equation (i) and (ii) , we get x=r . $cos α$
Similarly, we can have y=r . $cos β, z = r . cos γ$
$∴ - - \to O P = r cos α ˆ i + r cos β ˆ j + r cos γ . ˆ k$
Now, $- - \to O P . - - \to O P = {∣ ∣ ∣ - - \to O P ∣ ∣ ∣}^{2}$
$∴ {(r cos α)}^{2} + {(r cos β)}^{2} + {(r cos γ)}^{2} = r^{2}$
$\Rightarrow r^{2} ({cos}^{2} α + {cos}^{2} β + {cos}^{2} γ) = r^{2}$
$\Rightarrow {cos}^{2} α + {cos}^{2} β + {cos}^{2} γ = 1$
Consider ${sin}^{2} α + {sin}^{2} β + {sin}^{2} γ$
$= (1 - {cos}^{2} α) + (1 - {cos}^{2} β) + (1 - {cos}^{2} γ)$
$= 3 - ({cos}^{2} α + {cos}^{2} β + {cos}^{2} γ)$
$= 3 - 1 = 2$
$∴ {sin}^{2} α + {sin}^{2} β + {sin}^{2} γ = 2$ .

Updated on:21/07/2023

|

Class 12 MATHS JULY 2018

Topper's Solved these Questions

Similar Questions

Knowledge Check

If $α, β, γ$ are direction angles of a line , then $cos 2 α + cos 2 β + cos 2 γ =$
A $- 1$
B0
C1
D2
If $cos α, cos β, cos γ$ are the direction cosines of a line then the value of ${sin}^{2} α + {sin}^{2} β + {sin}^{2} γ$ is__________
A1
B2
C3
D4

GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERS- JULY 2018-SECTION II

Home
Ask Doubt
Profile