A satelite is revolving in a circular orbit at a height h above the surface of the earth of radius R. The speed of the satellite in its orbit is one-fourth the escape velocity from the surface of the earth. The relation between h and R is
h=2R
h=3R
h=5R
h=7R
The correct Answer is:D
According to the question,
vc=14ve
√GM(R+h)=14√2GMR
On taking square root both sides, we get
⇒ GMR+h=1162GMR
⇒ GMR+h=GM8R
⇒ R+h=8R
⇒ h=8R−R
⇒ h=7R
Topper's Solved these Questions
Similar Questions
A satellite is orbiting the earth in a circular orbit of radius r. Its
View SolutionA satellite is revolving in a circular orbit at a height 'h' from the earth's surface (radius of earth R, h ltltR). The minimum increase in its orbital velocity required, So that the satellite could escape from the erth's gravitational field, is close to :(Neglect the effect of atomsphere.)
View Solution
Knowledge Check
- Question 1 - Select One
An earth satellite of mass m revolves in a circular orbit at a height h from the surface of the earth. R is the radius of the earth and g is acceleration due to gravity at the surface of the earth. The velocity of the satellite in the orbit is given by
AgR2R+hBgRCgRR+hD√gR2R+h - Question 2 - Select One
A geostationary satellite is at a height h above the surface of earth. If earth radius is R-
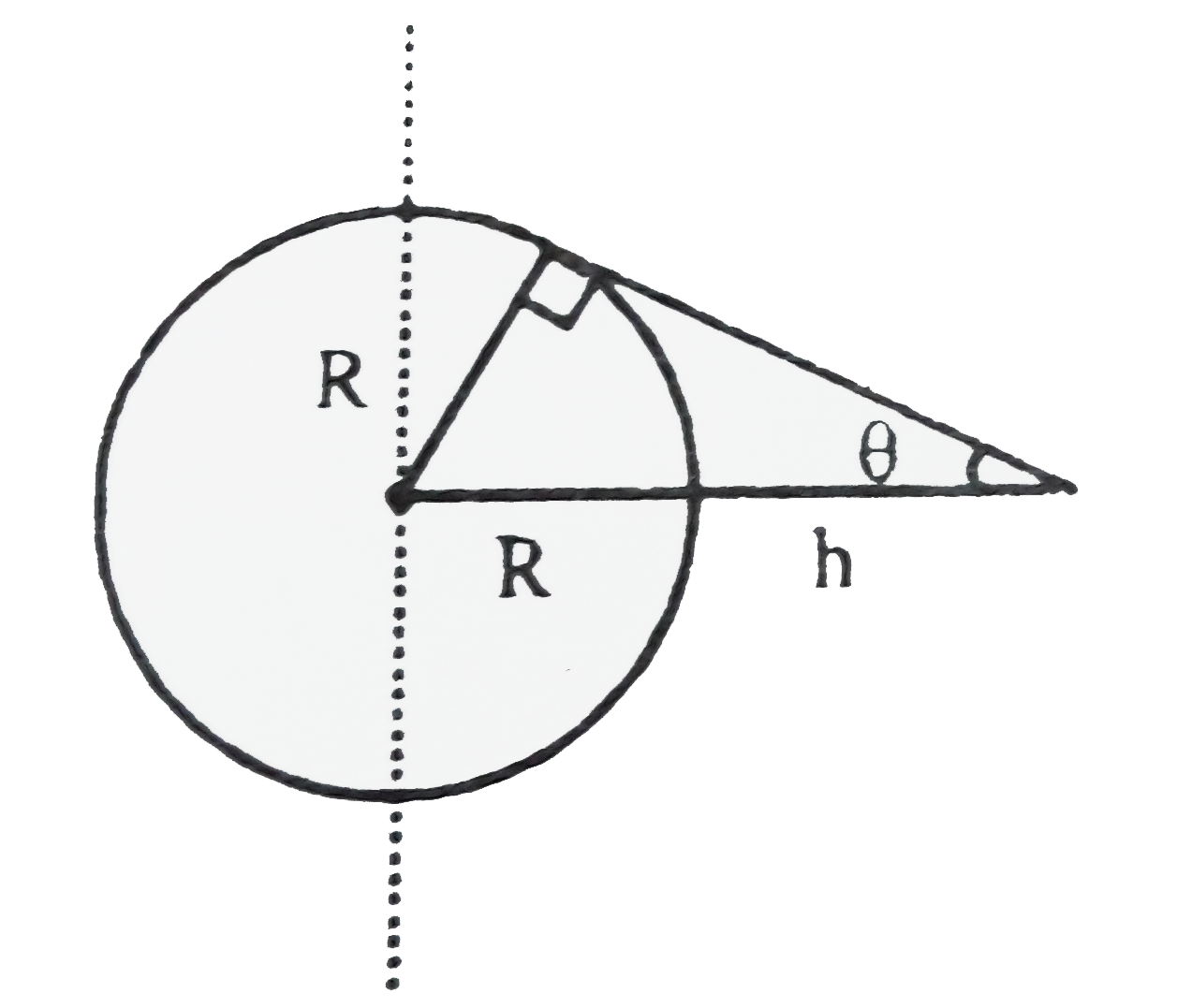 AThe minimum colatitude on earth upto which the satellite can be used for communication is sin−1(R/R+h)BThe maximum colatitudes on earth upto which the satellite can be used for communication is sin−1(R/R+h)CThe area on earth escaped from this satellite is given as (2πR2(1+sinθ))DThe area on earth escaped from this satellite is given as (2πR2(1+cosθ)
AThe minimum colatitude on earth upto which the satellite can be used for communication is sin−1(R/R+h)BThe maximum colatitudes on earth upto which the satellite can be used for communication is sin−1(R/R+h)CThe area on earth escaped from this satellite is given as (2πR2(1+sinθ))DThe area on earth escaped from this satellite is given as (2πR2(1+cosθ) - Question 3 - Select One
An artificial satellite is moving in a circular orbit around the earth with a speed equal to half the escape velocity from the earth of radius R. The height of the satellite above the surface of the earth is
ARBR/2C3 RD6 R
A geostationary satellite is orbiting the earth at a height of 5R above the surface of the earth, R being the radius of the earth. The time period of another satellite in hours at a height of 2R form the surface of the earth is
View SolutionAn artificial satellite is revolving in a circular orbit at height of 1200km above the surface of the earth. If the radius of the earth is 6400km and mass is 6×1024kg, the orbital velocity is
View SolutionA satellite is revolving in a circular orbit at a height 'h' from the earth's surface (radius of earth R, h ltltR). The minimum increase in its orbital velocity required, So that the satellite could escape from the erth's gravitational field, is close to :(Neglect the effect of atomsphere.)
View SolutionThe orbit velocity of a satellite at a height R above the surface of Earth is v. The escape velocity from the location is
View SolutionAn artificial satellite is orbiting at a height of 1800 km from the surface of earth. What is speed of the satellite ? (R = 6300 km)
View Solution

