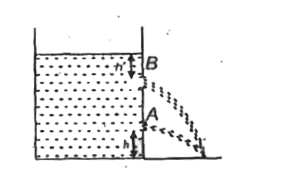
A vessel completely filled with water has holes 'A' and 'B' at depths 'h' and '2h' from the top, respectivel. Hole 'A' is a square of side 'L' and 'B' is circle of radish 'r' The water flowing out per second from both the holes is same Then, 'L'is equal to
r12(π)12(3)12
r⋅(π)14(3)14
r⋅(π)12(3)14
r12(π)13(3)12
The correct Answer is:C
Given, depth of hole A from the top = h Depth of hole B from the top =3h According to question, we can draw the following diagram

According the continuity equation,
Aava=A2v2
Velocity of efflux,
va=√2ght (for square hole
v2=√2g(3h)=√6gh (for circular hole)
L2√2gh=πr2√6gh
(∵area of square −L2area of circle=πr2)
On squaring both sides =, we get
2L4gh=6π2r4gh 2L4=6π2r4
L4=3π2r4 L=(3π2)1/4
L=rπ1/2(3)1/4
Topper's Solved these Questions
Similar Questions
A large open tank has two holes in the wall. One is a square hole of side L at a depth h from the top and the other is a circular hole of radius r at a depth 4h from the top. Whwn the tank is completely filled with water, the quantity of water flowing out per second from both the holes are the same. What is the value of r?
View SolutionA tank is filled with water and two holes A and B are made in it.- For getting same range, ratio of h'lh is
View Solution
Knowledge Check
A vessel completely filled with water has holes 'A' and 'B' at depths 'h' and '3h' from the top respectively. Hole 'A' is a square of side 'L' and 'B' is circle of radius 'r'. The water flowing out per second from both the holes is same. Then 'L' is equal to
Ar12(π)12(3)12Br(π)14(3)14Cr(π)12(3)14Dr12(π)13(3)12There are two holes P and Q at depths h and 4h from the top of a large vessel, completely filled with water. P is a square hole of side L and Q is a circular hole of radius r. If the same quantity of water flows out per second from both the holes, then the relation between L and r is
AL=r2BL=√2πrCL−2πrDL=√2πrA large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
A(a) L√2πB(b) 2πLC(c) LD(d) L2π
A closed vessel is half filled with water. There is a hole near the top of vessel and air is pumped out from this hole.
View SolutionA large open tank has two holes in its wall. Ine is a square hole of side a at a depath of x from the top and the other is a cirular hle of radius r at a depth 4x from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then r is equal to
View SolutionA large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
View SolutionIn a vessel containing water, a hole is made at a depth of 0.10 m from the free surface. What would be the velocity of efflux ?
View SolutionA hole is made in the bottom of a container having water filled up to a height h. The velocity of water flowing out of the hole is :
View Solution

