A frame made of metalic wire enclosing a surface area A is covered with a soap film. If the area of the frame of metallic wire is reduced by 50% the energy of the soap film will be changed by:
100%
75%
50%
25%
The correct Answer is:C
Surface energy = surface tension × surface area
E=T×2A
New surface energy,
E1=T×2(A2)=T×A
% decrease in surface energy
=E−E1E×100
=2TA−TA2TA×100=50%
Topper's Solved these Questions
Similar Questions
A rectagular wire frame with one movable side is convered by a soap film (fig.). What work (erg) will be done if this side of the frame is moved a distance S=2mm ? The length of the movable side is l=6cm. The surface tension of the soap film is α=40dyne/cm.
View SolutionA rectagular wire frame with one movable side is convered by a soap film (fig.). What force should be applied to the movable side to counterbalance it ? What work will be done if this side of the frame is moved a distance S=2cm ? The length of the movable side is l=6cm. The surface tension of the soap film is α=40dyne/cm.
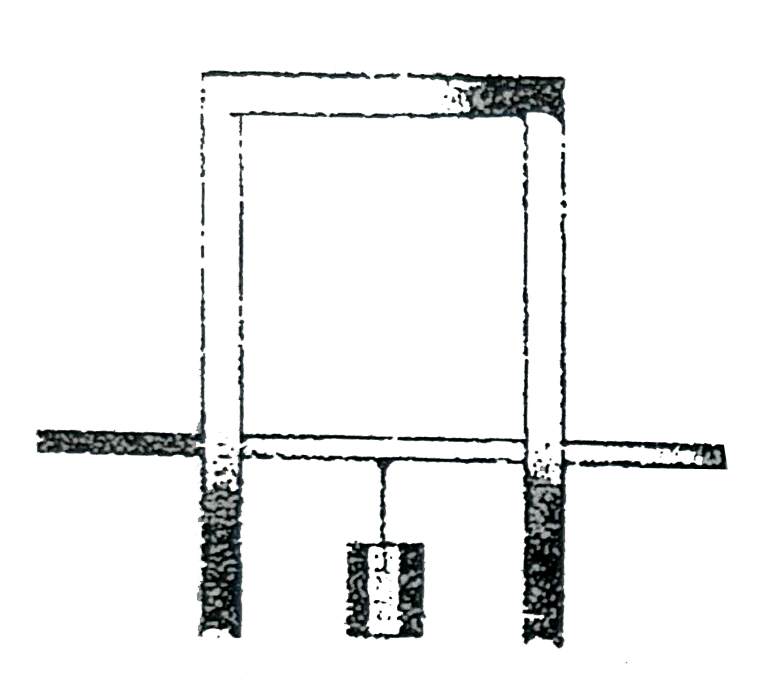
View Solution
Knowledge Check
A frame made of metallic wire enclosing a surface area A is covered with a soap film. If the area of the frame of metallic wire is reduced by 50% , the energy of the soap film will be changed by
A100%B75%C50%D25%A frame made of metallic wire enclosing a surface area A is covered with a soap film. If the area of the frame of metallic wire is reduced by 50% , the energy of the soap film will be changed by
A100%B75%C50%D25%A frame made of metallic wire enclosing a surface area A is covered with a soap film. If the area of the frame of metallic wire is reduced by 25%, the energy of the soap film will be changed by
A1B0.75C0.5D0.25
A frame made of a metallic wire enclosing a surface area A is covered with a soap film . If the area of the frame of metallic wire will be changed by
View SolutionIf area of cross-section of a metalic wire becomes n times, its resistance becomes
View SolutionIf the radius of sphere is reduced by 10%, then what will be the percentage change in its total surface area?
View SolutionThe area of cross-section of a metal wire is doubled, keeping its length same, then its resistance is:
View SolutionA circular frame made of 20 cm long thin wire is floating on the surface of water. If the surface tension of water is 70 dyne/cm. the required excess force to separate this frame from water will be :
View Solution
