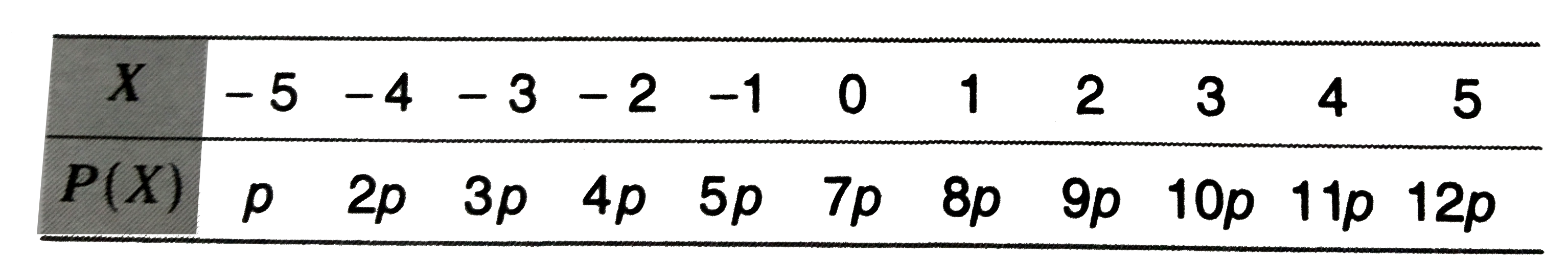If the probability density function of a random variable X is given as
then F(0) is equal to

A
P(X<0)
B
P(X>0)
C
1−P(X>0)
D
1−PX<0)
Video Solution
Text Solution
The correct Answer is:C
We know that, cumulative distribution function
F(x)=P(X≤x)
∴ F(0)=P(X≤0)
=P(x=0)+P(x=−1)+P(x=−2)
=0.15+0.3+0.2=0.65
(a) P(X<0)=P(x=−1)+P(x=−2)
=0.3+0.2=0.5
∴ P(X<0)≠F(0)
(b) P(X>0)=P(x=1)+P(x=2)
0.25+0.1=0.65
∴ P(X>0)≠F(0)
(c ) 1−P(X>0)=1−0.35=0.65
∴ 1−P(X>0)=F(0)
Hence, option (c ) is correct
|
Topper's Solved these Questions
- PROBABILITYBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PROBABILITYEXERCISE - Exercise 2 (MISCELLANEOUS PROBLEMS)
40 Videos
- PRACTICE SET 24BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PRACTICE SET 24EXERCISE - Paper 2 (Mathmatics)
50 Videos
- SEQUENCES AND SERIES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SEQUENCES AND SERIES EXERCISE - EXERCISE 31
1 Videos
Similar Questions
Knowledge Check
If the probability density function of a random variable X is f(x)=π2 in 0≤x≤2, then P(X>1.5X>1) is equal to
A716B34C712D2164If the probability density function of a random variable X is f(x)=x2 in 0≤x≤2, then P(X>1.5∣X>1) is equal to
A716B34C712D2164The probability distribution of a discrete random variable X is given below
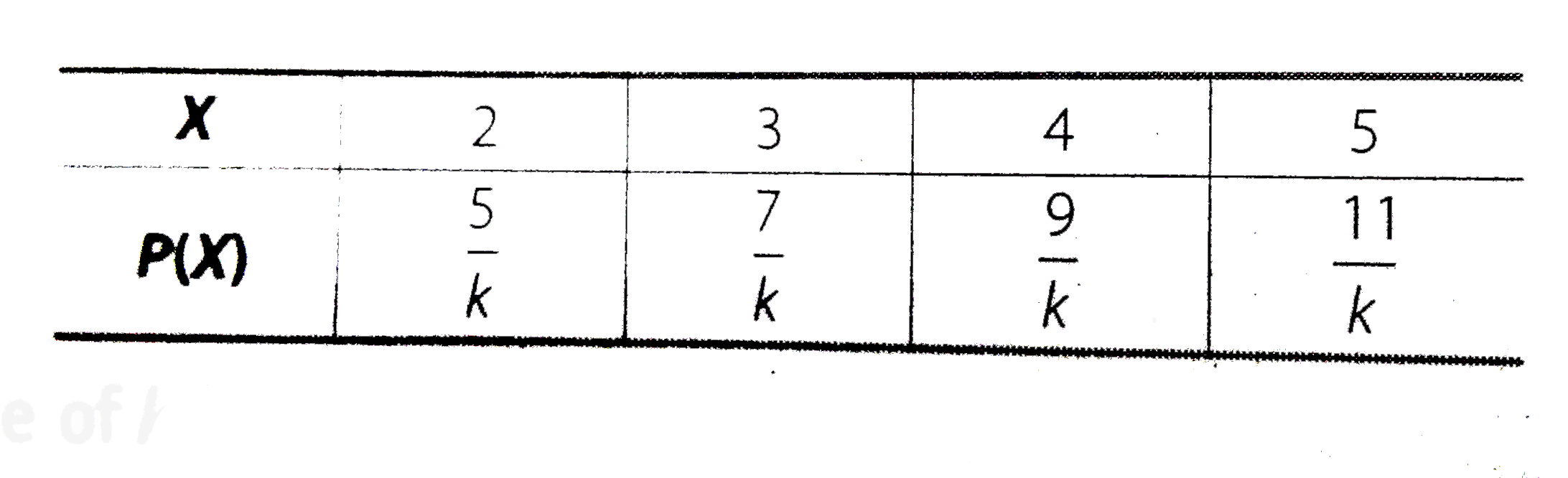
The value of k isA8B16C32D48
If f(x)= kx, 0 lt x lt 2 = 0 otherwise, is a probability density function of a random variable X , then find (i) value of k, (ii) P(1 lt x lt2).
View SolutionThe probability distribution of the random variable X is given by
Then, the value of V(X) is equal to

View SolutionIf the probability distribution of a random variable X is as given below
Then, mean and variance are

View SolutionConsider the probability distribution of a random variable X.

Variance of X
View SolutionThe probability distribution of a random variable X is given as follows:

If E(X)=2.3 , then value of k is
View Solution