Doubtnut Promotions Sticky

Find the equation of the perpendicular drawn from (2,4,-1) to the line x + 5 1 = y + 3 4 = z - 6 3 .

A

x - 2 6 = y - 4 3 = z + 1 2 , ( - 4 , 1 , - 3 )

B

x - 3 2 = y - 4 6 = ( z + 1 ) ( 2 ) , ( - 1 , 4 , 3 )

C

x + 3 6 = y - 4 3 = z - 2 2 , ( 3 , 4 , 1 )

D

x - 2 3 = y + 4 6 = z + 1 2 , ( 4 , 1 , 3 )

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

Any point on the line x + 5 1 = y + 3 4 = z - 6 - 9 = λ is given by M ( λ - 5 , 4 λ - 3 , - 9 λ + 6 ) .
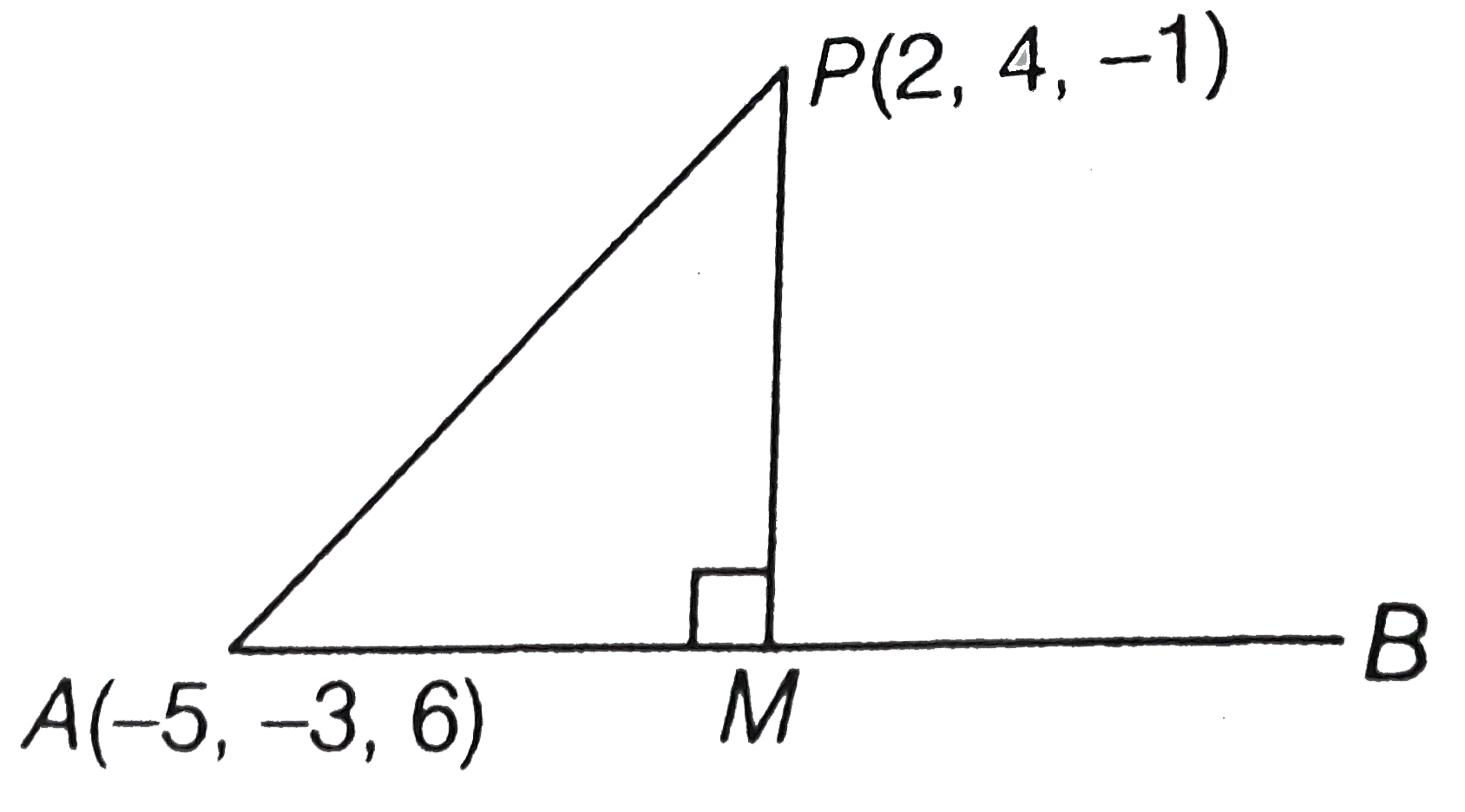
ocr_image
The direction ratios of the line PM are
( 2 - λ + 5 , 4 - 4 λ + 3 , - 1 + 9 λ - 6 )
i.e., ( 7 - λ , 7 - 4 λ , - 7 + 9 λ )
since, PM is perpendicular to AM, we have
1 ( 7 - λ ) + 4 ( 7 - 4 λ ) - 9 ( - 7 + 9 λ ) = 0
⇒ 7 - λ + 28 - 16 λ + 63 - 81 λ = 0
⇒ 98 - 98 λ = 0 ⇒ λ = 1
∴ The point is M ( - 4 , 1 , - 3 )
Equation of the perpendicular is
x - 2 - 4 - 2 = y - 4 1 - 4 = z + 1 - 3 + 1
⇒ x - 2 6 = y - 4 3 = z + 1 2

|
Updated on:21/07/2023
Class 12MATHSLINE

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Find the equation of the perpendicular drawn from the point (2,4,−1) to the line x+5=14(y+3)=−19(z−6) and obtain the co-ordinates of the foot of this perpendicular

    Ax−26=y−43=z+12,(−4,1,−3)
    Bx−32=y−46=z+12,(−1,4,3)
    Cx+36=y−43=z−22,(3,4,1)
    Dx−23=y+46=z+12,(4,1,3)
  • Question 2 - Select One

    The foot of the perpendicular from (2,4,-1) to the line x+51=y+34=z−6−9 is

    A(-4,1,-3)
    B(4,-1,-3)
    C(-4,-1,3)
    D(-4,-1,-3)
  • Question 3 - Select One

    Find the distance of a point (2,4,−1) from the line
    x+51=y+34=z−6−9.

    A3
    B5
    C7
    D9