Let A(1,−1,2)andB(2,3−1) be two points. If a point P divides AB internally in the ratio 2:3, then the position vector of P is
A
1√5(ˆi+ˆj+ˆk)
B
1√3(ˆi+6ˆj+ˆk)
C
1√3(ˆi+ˆj+ˆk)
D
15(7ˆi+3ˆj+4ˆk)
Video Solution
Text Solution
The correct Answer is:D
α=2.2+3.12+3=75
β=2.3+3.(−1)2+3=35
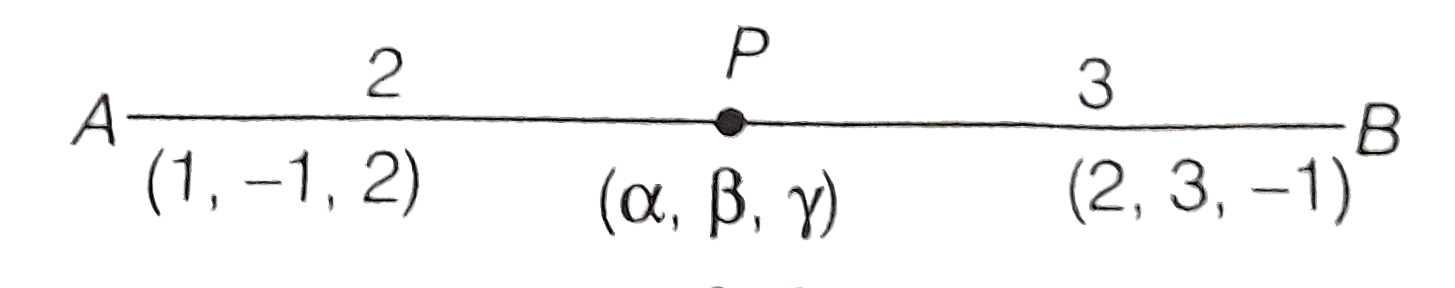
and γ=2(−1)+3.22+3=45
∴OP=15(7ˆi+3ˆj+4ˆk)
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the position vector of a point A is →a+2→band→a divides AB in the ratio 2:3, then the position vector of B, is
A2a−bBb−2aCa−3bDbIf the position vector of a point A is →a+2→band→a divides AB in the ratio 2:3, then the position vector of B, is
A2a−bBb−2aCa−3bDbA variable line through the point (65,65) cuts the coordinate axes at the points A and B respectively. If the point P divides AB internally in the ratio 2:1, then the equation of the locus of P is
A5xy=(2x+y)B5xy=2(2x+y)C5xy=(x+2y)D5xy=2(x+2y)
The position vector of two points A and B are 6→a+2→b and →a−3→b. If point C divides AB in the ratio 3:2 then show that the position vector of C is 3→a−→b
View SolutionIf a and b are position vector of two points A,B and C divides AB in ratio 2:1, then position vector of C is
View SolutionIf the position vector of p is 3¯p+¯qand¯p divides PQ internally in the ratio 3:4, the position vector of Q is
View SolutionIf the position vector of a point A is →a+2→band→a divides AB in the ratio 2:3, then the position vector of B, is
View SolutionThe position vectors of the point which divides internally in the ratio 2:3 the join of the points 2¯a−3¯band3¯a−2¯b, is
View Solution