Two identical metal plates are given poistive charges Q1 and Q2 (<Q1) respectively. If they are now brought close together to form a parallel plate capacitor with capacitance C, the potencial difference between them is
(a) (Q1+Q2)/(2C)
(b) (Q1+Q2)/C
(c) (Q1−Q2)/C
(d) (Q1−Q2)/(2C)
The correct Answer is:D
To find the potential difference between two identical metal plates with positive charges Q1 and Q2 (where Q1>Q2), we can follow these steps:
Step 1: Understand the Electric Field
When two charged plates are brought close together, they create an electric field between them. The electric field E due to a charged plate is given by the formula:
E=Qϵ0A
where Q is the charge on the plate, ϵ0 is the permittivity of free space, and A is the area of the plate.
Step 2: Calculate Electric Fields from Each Plate
For the plate with charge Q1:
E1=Q1ϵ0A
For the plate with charge Q2:
E2=Q2ϵ0A
Step 3: Determine the Net Electric Field
Since both plates are positively charged, the electric fields will point away from each plate. The net electric field E between the plates can be calculated as:
E=E1−E2=Q1ϵ0A−Q2ϵ0A=Q1−Q2ϵ0A
Step 4: Relate Electric Field to Potential Difference
The potential difference V between the plates is related to the electric field by the formula:
V=E⋅d
where d is the distance between the plates.
Step 5: Substitute the Expression for Electric Field
Substituting the expression for E into the potential difference formula gives:
V=(Q1−Q2ϵ0A)⋅d
Step 6: Use the Capacitance Formula
The capacitance C of a parallel plate capacitor is given by:
C=ϵ0Ad
From this, we can express 1C:
1C=dϵ0A
Step 7: Substitute Capacitance into the Potential Difference Equation
Now we can rewrite the potential difference in terms of capacitance:
V=(Q1−Q2)⋅1C
Final Result
Thus, the potential difference V between the plates is:
V=Q1−Q2C
When two charged plates are brought close together, they create an electric field between them. The electric field E due to a charged plate is given by the formula:
E=Qϵ0A
where Q is the charge on the plate, ϵ0 is the permittivity of free space, and A is the area of the plate.
For the plate with charge Q1:
E1=Q1ϵ0A
For the plate with charge Q2:
E2=Q2ϵ0A
Since both plates are positively charged, the electric fields will point away from each plate. The net electric field E between the plates can be calculated as:
E=E1−E2=Q1ϵ0A−Q2ϵ0A=Q1−Q2ϵ0A
The potential difference V between the plates is related to the electric field by the formula:
V=E⋅d
where d is the distance between the plates.
Substituting the expression for E into the potential difference formula gives:
V=(Q1−Q2ϵ0A)⋅d
The capacitance C of a parallel plate capacitor is given by:
C=ϵ0Ad
From this, we can express 1C:
1C=dϵ0A
Now we can rewrite the potential difference in terms of capacitance:
V=(Q1−Q2)⋅1C
Thus, the potential difference V between the plates is:
V=Q1−Q2C
Topper's Solved these Questions
- ELECTROSTATICSBook:SUNIL BATRA (41 YEARS IITJEE PHYSICS)Chapter:ELECTROSTATICSExercise:Subjective Problems
Explore 2 Videos
- ELECTROSTATICSBook:SUNIL BATRA (41 YEARS IITJEE PHYSICS)Chapter:ELECTROSTATICSExercise:Comprehension Based Questions
Explore 2 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBook:SUNIL BATRA (41 YEARS IITJEE PHYSICS)Chapter:ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTExercise:JEE Main And Advanced
Explore 107 Videos
- MODERN PHYSICSBook:SUNIL BATRA (41 YEARS IITJEE PHYSICS)Chapter:MODERN PHYSICSExercise:MCQ (One Correct Answer
Explore 1 Video
Similar Questions
If a thin metal foil of same area is placed between the two plates of a parallel plate capacitor of capacitance C, then new capacitance will be
View SolutionTwo plates ( area =s ) charged to +q1 and +q2(q2<q1) are brought closer to form a capacitor of capacitance C. The potential difference across the plates is
View Solution
Knowledge Check
Two identical metal plates are given positive charges Q1 and Q2 (<Q1) respectively. If they are now brought close together to form a parallel plate capacitor with capacitance C, the potential difference between them is :
AQ1+Q22CBQ1+Q2CCQ1−Q2CDQ1−Q22CTwo identical metal plates are given positive charges Q1 and Q2 (<Q1) respectively. If they are now brought close together to form a parallel plate capacitor with capacitance C, the potential difference between them is :
AQ1+Q22CBQ1+Q2CCQ1−Q2CDQ1−Q22CIn an isolated parallel plate capacitor of capacitance C, the plates have charge Q1 and Q2. The potential difference between the plates is
AQ1+Q22CBQ1−Q22CCQ12CD−Q22C
When a metal slab is placed between the charged identical , parallel plates , the potential difference between the plates
View SolutionThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View SolutionThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
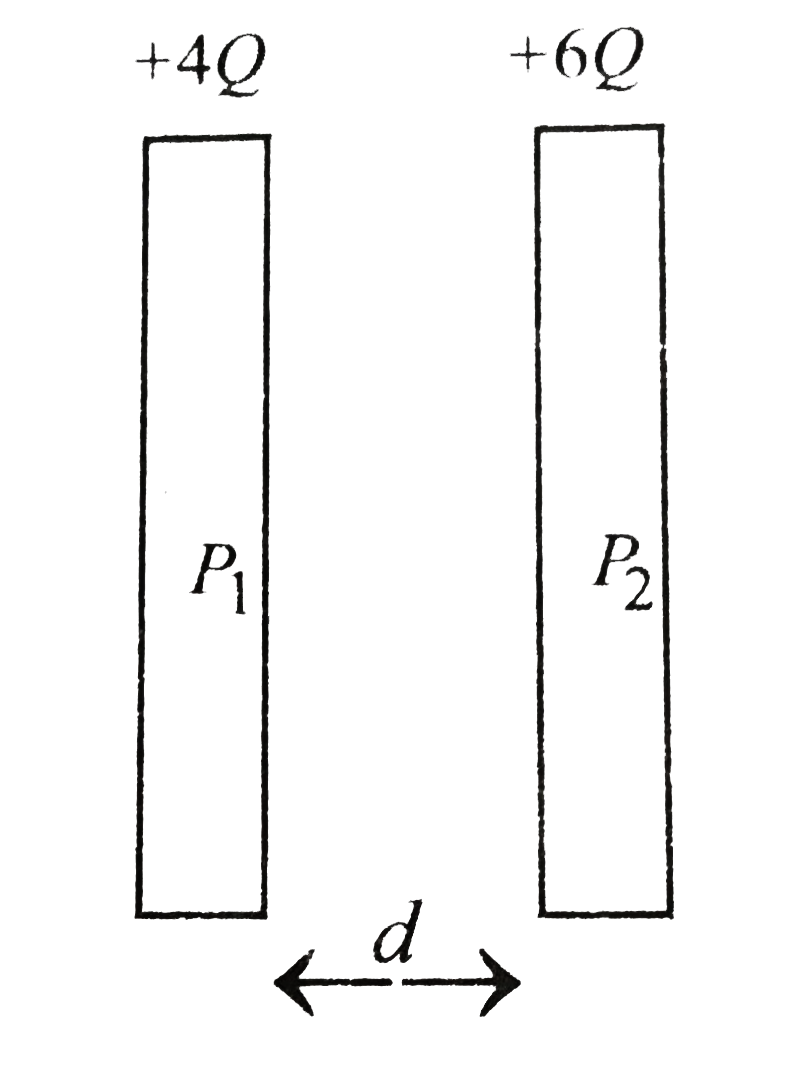
View SolutionTwo identical conducting very large plates P1andP2 having charges +4Qand+6Q are placed very closed to each other at separation d. The plate area of either face of the plate is A. The potential difference between plates P1andP2 is
View SolutionA parallel plate capacitor C has a charge Q. The actual charges on its plates are
View Solution

