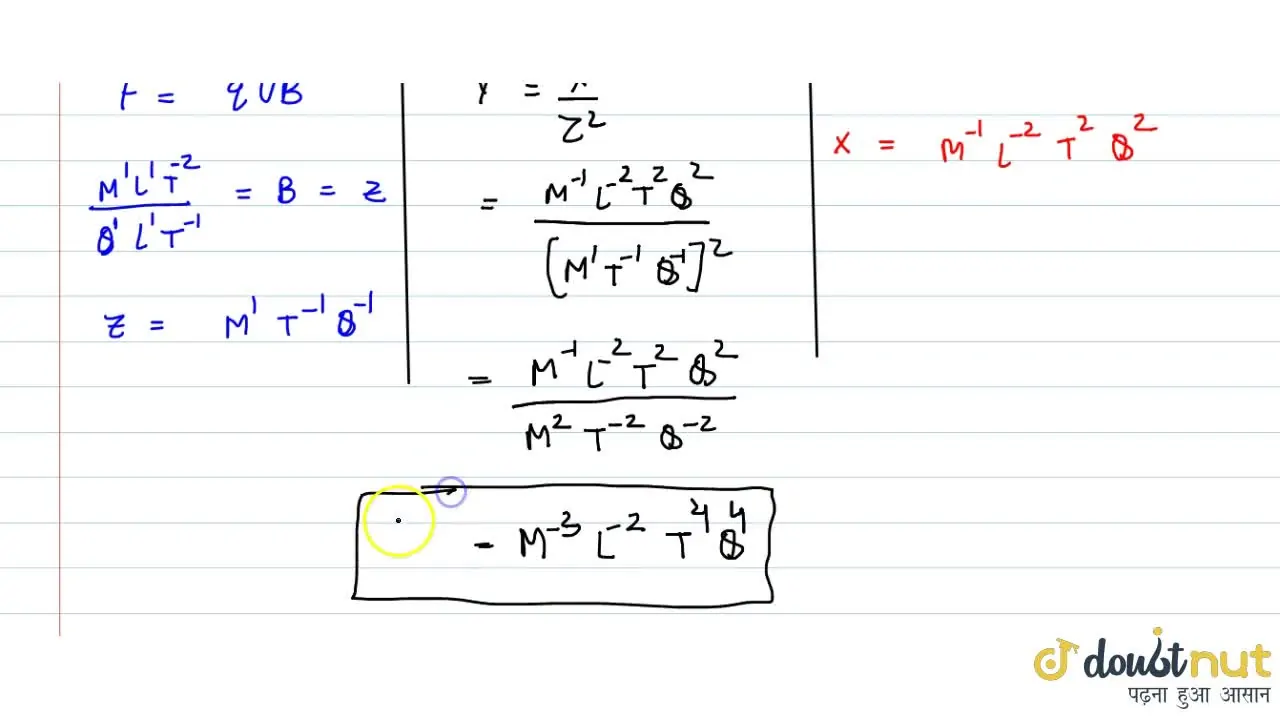
In the formula X=3YZ2,XandZ have dimensions of capacitance and magnetic induction respectively. The dimensions of Y in MKSQ system are ………………, ………………….
The correct Answer is:B, C, D
[X]=[C]=[M−1L−2T2Q2]
[Z] = [B] = [MT^(-1)Q^(-1)]<br>∴[Y] = [M^(-1)L^(-2)T^(2)Q^(2)]/[MT^(-1)Q^(-1)]^(2)=[M−3L−2T4Q4]
Related Playlists
Similar Questions
In the formula X=3YZ2,XandZ have dimensions of capacitance and magnetic induction respectively. The dimensions of Y in MKSQ system are ………………, ………………….
View SolutionIn the fromla X=1YZ2, X and Z have dimensions of capacitance and amgnetic induction, respectively. The dimension of Y in MKSQ system are
View SolutionIn the formula X=3YZ2, X and Z have dimensions of capacitance and magnetic induction respectively. The dimensions of Y in MKSQ system should be
View Solution(a) In the formula X=3YZ2, X and Z have dimensions of capcitnce and magnetic inlduction, respectively. What are the dimensions of Y in MKSQ system?
(b) A qunatity X is given by ε0 L (Δ)V(Δ)r, where ε0 is the permittivity of free space, L is a lenght, ΔV is a potential difference and Δt is a time interval. Find the dimensions of X.
(c) If E,M,J and G denote energy , mass , angular momentum and gravitational constant, respectively. find dimensons of EJ2M5G2
(d) If e,h,c and ε0 are electronic charge, Planck 's constant speed of light and permittivity of free space. Find the dimensions of e22ε0hc.View SolutionIn the formula X=3YZ^2, X and Z have dimeniosn of capacitance and magnetic induction respectively. The dimensions of Y in MKSQ system are
View SolutionIn the formula X=3YZ2 , X and Z have dimensions of capacitance and magteic induction respectively . When are the dimensions of F in MESQ system ?
View SolutionIn the formula X=5YZ2, X and Z have dimensions of capacitance and magnetic field, respectively. What are the dimensions of Y in SI units?
View Solution(a) In the formula X=3YZ2, X and Z have dimensions of capcitnce and magnetic inlduction, respectively. What are the dimensions of Y in MKSQ system?
(b) A qunatity X is given by ε0 L (Δ)V(Δ)r, where ε0 is the permittivity of free space, L is a lenght, ΔV is a potential difference and Δt is a time interval. Find the dimensions of X.
(c) If E,M,J and G denote energy , mass , angular momentum and gravitational constant, respectively. find dimensons of EJ2M5G2
(d) If e,h,c and ε0 are electronic charge, Planck 's constant speed of light and permittivity of free space. Find the dimensions of e22ε0hc.View SolutionIn the forumla a=3bc2'a' and 'c' have dimensions of electric capacitance and magnetic induction, respectively, what are dimensions of 'b' in MKS system?
View SolutionIn the formula, X=3YZ2, X has dimensions of capacitance and Z has dimensions of magnetic induction. The dimensions of Y are
View Solution