Prove that If two chords of a circle intersect internally then the product of the length of the segments are equal.
Data:AB and CD are chords of a circle intersecting internally at P.To Prove:AP x BP = CP x DP.Construction:Join AC and BD.Proof:
Related Solutions
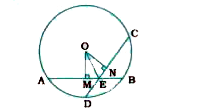
If two equal chords of a circle intersect within the circle, prove that
the segments of one chord are equal to corresponding segments
of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments ofone chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to correspondig segments of the other chord.
View Solutionयदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के खण्ड दूसरी जीवा के संगत खण्डों के बराबर हैं |
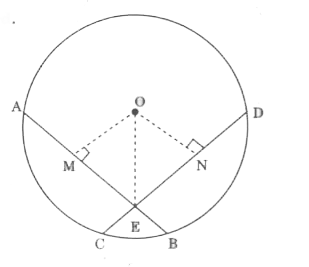
View SolutionIf two equal chords of a circle in intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that : the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View Solutionयदि एक वृत्त की दो समान लम्बाई की जिवाएँ वृत्त के अंदर प्रतिच्छेद करती हो, तो सिध्द करो कि :
(i) एक जीवा के खंड दूसरी जीवा के संगत खंडो के बराबर होते है ।
(ii) प्रतिच्छेद बिन्दु को केंद्र से मिलाने वाली रेखा, जीवाओ से बराबर कोण बनाती है ।
View SolutionIf two equal chords of a circle in intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that : the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionTheorem of internal division of chords.
Suppose two chords of a circle intersect each other in the interior of the circle, then the product of the lengths of the two segments of one chord is equal to the product of the lengths of the two segments of the other chord.
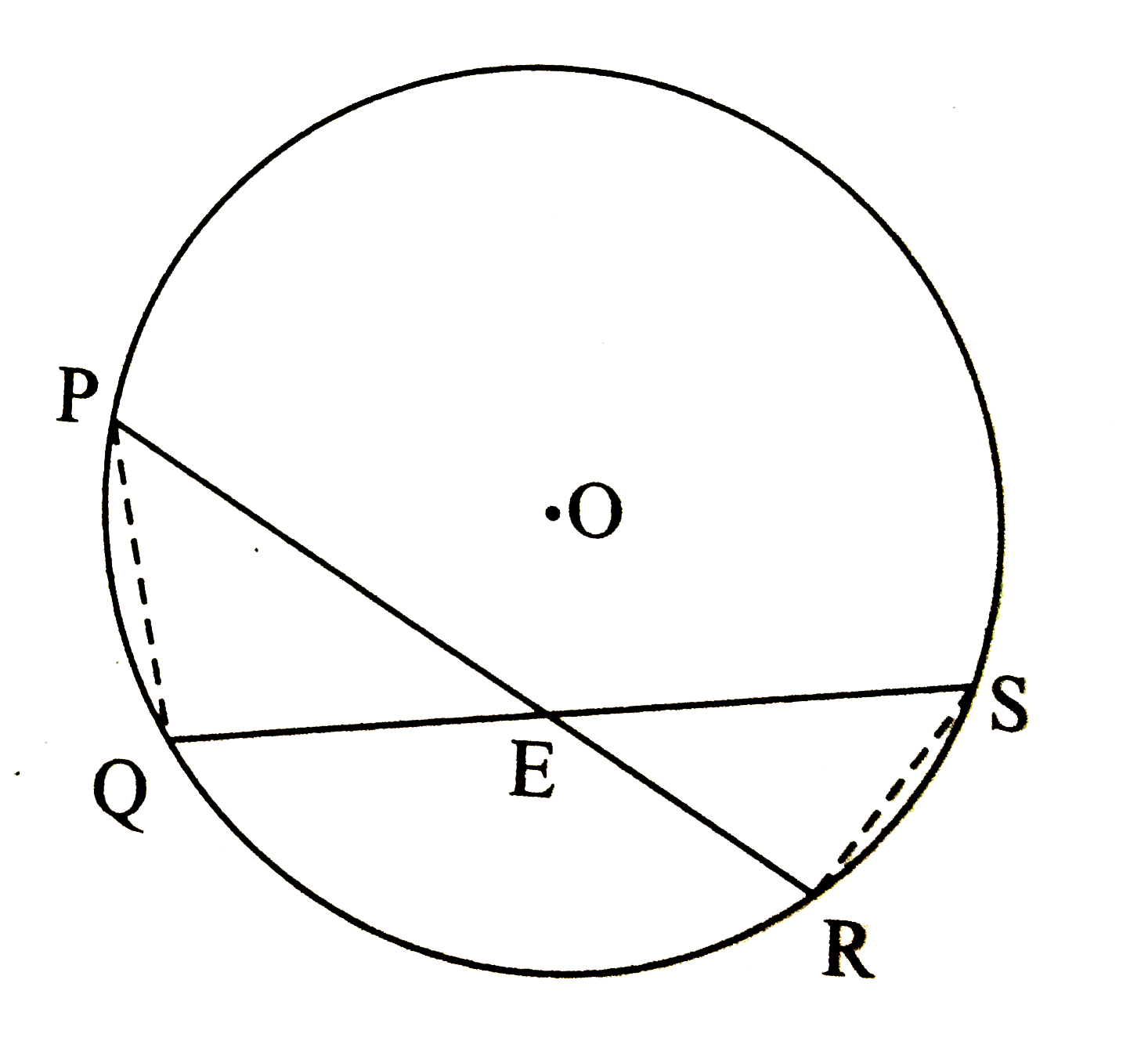
Given (1) A circle with centre O .
(2) chords PR and QS intersect at point E inside the circle.
To prove PE ER = QE xx ES : Draw seg PQ and seg RS
View Solutionसिद्ध कीजिए किसी वृत्त की दो बराबर जीवाओं के प्रतिच्छेदन बिन्दु को केन्द्र से मिलाने वाला रेखाखण्ड, जीवाओं से अन्तरित कोण को अर्द्धित करता है।
View SolutionIf two equal chords of a circle intersect, then prove that two parts of one chord are separately equal to the two parts of the other chord.
View SolutionIf two intersecting chords of a circle make equal angles with the diameterpassing through their point of intersection, prove that the chords are equal
View Solution