In the circuit shown above. the battery has been connected for a long time so that the currents have steady values. Given these conditions calculate each of the followinga. The current in the 9-ohm resistor.b. The current in the 8-ohm resistor.c. The potential difference across the 30-microfarad capacitor.d. The energy stored in the 30-microfarad capacitor.
a. In their steady states no current flows through the capacitor so the effective resistance of the branch on the right is 8 Ω + 4 Ω = 12 Ω. This is in parallel with the 4 Ω resistor making their effective resistance 12 × 4/12 + 4 = 3 Ω. Adding the 9 Ω resistor in the main branch gives a total circuit resistance of 12 Ω and a total current of ε/R = 10 A. This is the current in the 9 Ω resistor as it is in the main branch.b. With 10 A across the 9 Ω resistor the potential drop across it is 90 V leaving 30 V across the two parallel branches on the right. With 30 V across the 12 Ω effective resistance in the right branch we have a current through that branch including the 8 Ω resistor of V/R = 2.5 A
Related Solutions
Calculate the steady state current in the 2- ohm resistor shown in the circuit in the figure. The intermal resistance of the battery is negligible and the capacitance of the condenser C is 0.2 microfarad.
View SolutionCalculate the steady state current in the 2- ohm resistor shown in the circuit in the figure. The intermal resistance of the battery is negligible and the capacitance of the condenser C is 0.2 microfarad.
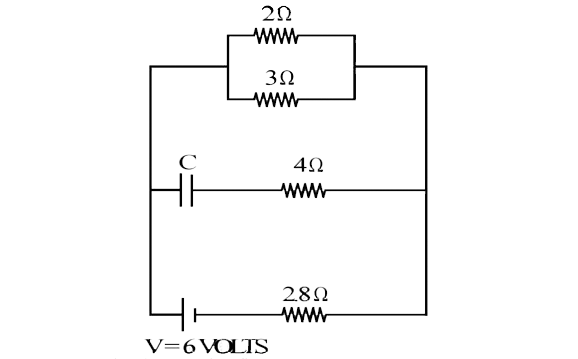
View Solutionदिये गये परिपथ में प्रारम्भिक अवस्था में स्विच है तथा संधारित्र अनावेशित है प्रत्येक संधारित्र की धारिता 2 माइक्रोफैरड है तथा प्रतिरोधों का मान 1 ओम है।
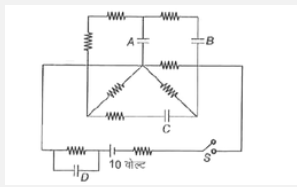
लम्बे समय के पश्चात बैटरी से प्रवाहित धारा का मान होगा।
View SolutionIn the circuit diagram suppose the resistors , and have the values of 5 ohm, 10 ohm and 30 ohm respectively. Which have been connected to a battery of 12 V.
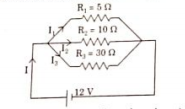
Calculate the current through each resistor?
View SolutionIn a series C- R circuit R = 30 ohms C = 0.25 microfarad, e.m.f. (electromotive force) = 100 volts and co = 10,000 radian/second. Find the current in the circuit and calculate voltage across resistor and the capacitor.
View SolutionIn a series RC circuit, R = 30 ohm, C = = 100 V, . Find the current in the circuit and calculate the voltage across the resistor and capacitor. Is the algebraic sum of these voltages more than the source voltage ? If yes, resolve the paradox.
View SolutionObtain an expression for the power in a.c. circuit containing a resistance and capacitance in series.
View SolutionIn the circuit diagram suppose the resistors , and have the values of 5 ohm, 10 ohm and 30 ohm respectively. Which have been connected to a battery of 12 V.
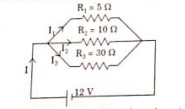
the total current in the circuit?
View SolutionIn the given circuit, in steady state 2muF Calculate the potential difference across the capacitor. If the internal resistance of the battery is 1 ohm.
View SolutionIn the given circuit, with steady current, calculate the potential difference across the capacitor and the charge stored in it.
View Solutionएक संधारित्र जिसके श्रेणीक्रम में एक 30 ओम का प्रतिरोध जुड़ा है, प्रत्यावर्ती धारा-स्रोत से जुड़ा है। संधारित्र का प्रतिघात 40 ओम है। धारा तथा सप्लाई वोल्टेज के बीच कलान्तर ज्ञात कीजिए।
View SolutionIn the given circuit, with steady current, the potential difference across the capacitor is
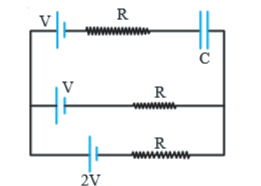
View SolutionIn the given circuit, with steady current, the potential difference across the capacitor is

View Solution50 हर्ट्ज आवृत्ति का प्रत्यावर्ती वोल्टेज ऐसे परिपथ में लगाया जाता है जिसमे 20 ओम प्रतिरोध, 100 मिली हेनरी प्रेरकत्व तथा 30 माइक्रोफैरड संधारित्र श्रेणीक्रम में लगे है | परिपथ में धारा वोल्टेज से कितना अग्रगामी अथवा पश्चगामी है ?
View Solutionएक 60 माइक्रोफैरड का संधारित्र एक 110 वोल्ट तथा 60 हर्ट्स के (AC supply) प्रत्यावर्ती धारा स्रोत से जुड़ा है। परिपथ में धारा के वर्ग-माध्य-मूल मान की गणना करो
View SolutionAn ideal inductor of 1 H is connected across a resistance of 100 ohm as shown in the figure. What is the potential difference across the 100 ohm resistance, when the current has attained a steady value?
View SolutionA resistance of 6 ohms is connected in series with another resistance of 4 ohms. A potential difference of 20 volts is applied across the combination. Calculate the current through the circuit and potential difference across the 6 ohm resistance.
View SolutionIn the circuit shown , the value of R in ohm that will result in no current through the 30 V battery is
View SolutionIn the circuit shown , the value of R in ohm that will result in no current through the 30 V battery is
View SolutionA current of 2A flows through a 2 ohm resistor when connected across a battery , the same battery supplies a current of 0.5A when connected across a 9 ohm resistor . the internal resistance of the battery is
View Solution