Derive the formula expressing molar heat capacity of a unidimensional crystal a chain of identical atoms as a function of temperature T if the Debye temperature of the chain is equal to θ. Simplify the obtained expression for the case T >> θ.
In the Debye approximation the number of modes per unit frequency interval is given by
Related Solutions
Derive the formula expressing molar heat capacity of a unidimensional crystal, a chain of identical atoms, as a function of temperature T if the Debye temperature of the chain is equal ot Theta . Simplyfie the octained expression for the case Tgt Theta
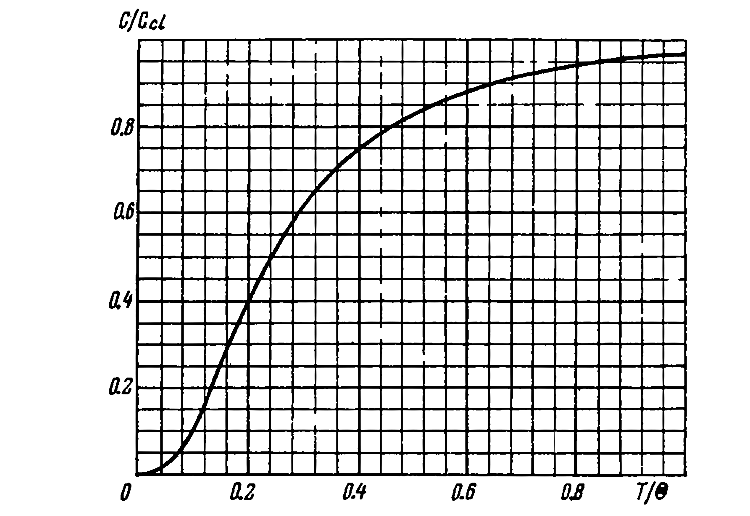
View SolutionFigure. 6.10 shows heat capacity of a crystal vs temperatue in terms of the Debye theory. Here is classical heat capacity is the Debye temperature. Using this plot, find:
(a0 The Debye temperature for silver if at a temperature its molar heat capacity is equal to ,
(b) the molar heat capacity of aluminum at if at it is equal to
(c )the maximum vibration frequency for copper whose heat capacity at differs form the classical value by .
View SolutionDemostrate that molar heat capacity of a crystal at a temperature , where is the Debye temperature, is defined by Eq. (6.4f)
View SolutionProve the identity (sin θ + cos θ)(tan θ + cot θ) = sec θ + cosec θ
View SolutionAssuming the propagation velocities of longitudinal and transverse vibrations to be the same and equal to , find the Debye temperature
(a) for a unidimensional crystal, i.e., a chain identical atoms, incorporating atoms per unit length,
(b) for a two-dimensional crystal, i.e., a plance square grid consisting of identical atoms, containing atoms per unit area,
(c ) for a simple cubic lattice consisting of identical atoms, containing atoms per unit volume.
View SolutionAt very low temperatures the heat capacity of crystals os equal to C = aT^3 , where a is a constant. Find the entropy of a crystal as a function of temperature in this temperature interval.
View SolutionDraw the vibration energy of a crystal as a function of frequency (neglecting the zero-point vibrations). Consider two cases: T= Theta//21 and T=Theta//4 , where Theta is the Debye temperature.
View SolutionAccording to Debyes law the specific heat at extremely low temperatures value with temperature T as
View SolutionAccording to Debye s law the specific heat at extremely low temperatures value with temperature T as
View SolutionSimplify: is equal to
View Solutionताप T पर एन्ट्रोपी परिवर्तन को निम्न प्रकार से व्यक्त किया जा सकता है -
View SolutionIf the thermal conductivity at absolute temperature T is sigma expressed by
View SolutionT(nπ±θ): Allied Angle Changing Rules
View SolutionWhat is the most likely value for (molar heat capacity at constant temperature) ?
View Solution√(1+sin θ) ( 1 - sin θ) is equal to
View Solution(1 + cot2 θ) (1 – cos θ) (1 + cos θ) = …………………. (a) tan2 θ – sec2 θ (b) sin2 θ – cos2 θ (c) sec2 θ – tan2 θ (d) cos2 θ – sin2 θ
View SolutionDerive expression for heat produced by the AC source in time t.
View SolutionMolar heat capacity of a gas at constant temperature and pressure is:
View SolutionThe molar heat capacity for a gas at constant and is
View Solution