A spider and a fly are on the surface of a glass sphere. Where must the fly be for-the spider to be able to see it? Assume that the radius of the sphere is much larger than the sizes of the spider and the fly. The refractive index of glass is ngl = 1.43.
Let the spider be at point A Fig. 236 located above the upper point D of the sphere. The spherical surface corresponding to the arc BDB of the circle is visible to the spider. Points Band B are the points of intersection of tangents drawn from point A to the surface of the sphere. The ray AB propagates within the sphere along BC. The angle α can be found from the conditionwhere no i s the refractive index of glass. This ray will emerge from the sphere along CA Therefore the fraction of the spherical surface corresponding to the arc CDC will also be visible by way of an example the optical path of the ray AKLM is shown.The surface of the spherical zone corresponding to the arcs BC and BC will be invisible to the spider.The angle γ is determined from the conditionwhere R is the radius of the sphere and h is the altitude of the spider above the spherical surface. Since R >> h by hypothesis γ ≈ 0. We note now that β = pi - 2α and sin α = 1/ngl. Therefore Thus the opposite half of the spherical surface is visible to the spider and the fly must be there.
Related Solutions
A spider and a fly are on the surface of a glass sphere. As the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it? Assume that the radius of the sphere (R) is much larger than the sizes of the spider and the fly. take the refractive index of glass to be equal to .
View SolutionA spider and a fly are on the surface of a glass sphere. As the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it? Assume that the radius of the sphere (R) is much larger than the sizes of the spider and the fly. take the refractive index of glass to be equal to .
View SolutionA spider and a fly are on the surface of a glass sphere. As the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it? Assume that the radius of the sphere (R) is much larger than the sizes of the spider and the fly. take the refractive index of glass to be equal to .
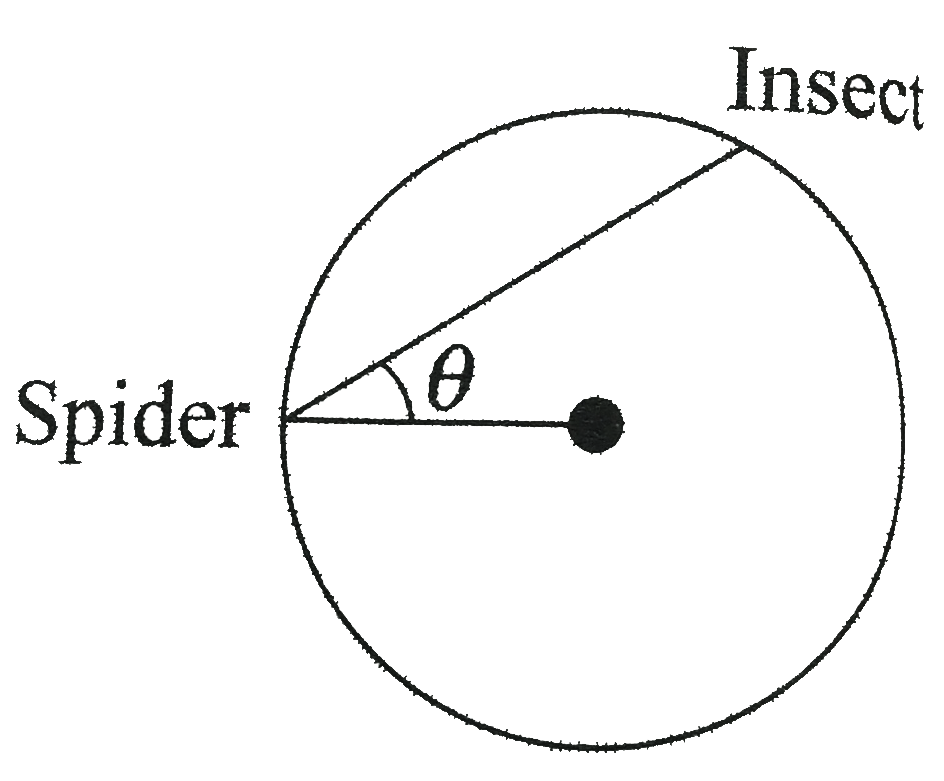
View SolutionA spider is on the surface of a glass sphere with a refractive inndex of 1.5 . An insect crawls on the other side of the sphere as shown in Fig. For what maximum value of theta will the spider be able to still see the insect. Assume the spiders eye is in air.
View SolutionA spider is on the surface of a glass sphere with a refractive inndex of . An insect crawls on the other side of the sphere as shown in Fig. For what maximum value of will the spider be able to still see the insect. Assume the spiders eye is in air.
View SolutionCrustaceans, insects and spiders are able to regenerate their
View SolutionCrustaceans, spiders and insects are able to regenerate their
View SolutionCrustaceans, spiders and insects are able to regenerate their
View SolutionCrustaceans, spiders and insects are able to regenerate their
View SolutionA spider is hanging by means of its own silk thread directly above a transparent fixed sphere of radius R=20cm as shown in the figure. The refractive index of the material of the sphere is equal to sqrt(2) and the height of the spider from the centre of the sphere is 2R(=40cm) . An insect, initially sitting at the bottom, starts crawling on the sphere along a vertical circular path with the constant speed of pi//4 cm//s . For how long time the insect will be invisible for the spider, assume that it crawls once round the vertical circle.
View SolutionAll spiders weave webs, which help them in three things. The webs help the spiders to lay eggs, hide and catch food. Many spiders prefer to lay their eggs in their webs, in which their eggs stay together and secure. The webs are sticky and thus they help the spiders in catching the food. When an insect comes flying in the web, it gets trapped, moves here and there, tries to get out but cannot do so because it is trapped. The spider knows that the insect is trapped because they feel the web move and the spider reaches the insect. Without webs the spider would not be able to live as it does. Spiders need webs to survive, but if you can't find webs in your home, it doesn't mean that your house is free of spiders. How do spiders know that their prey is trapped in their web?
View SolutionAll spiders weave webs, which help them in three things. The webs help the spiders to lay eggs, hide and catch food. Many spiders prefer to lay their eggs in their webs, in which their eggs stay together and secure. The webs are sticky and thus they help the spiders in catching the food. When an insect comes flying in the web, it gets trapped, moves here and there, tries to get out but cannot do so because it is trapped. The spider knows that the insect is trapped because they feel the web move and the spider reaches the insect. Without webs the spider would not be able to live as it does. Spiders need webs to survive, but if you can't find webs in your home, it doesn't mean that your house is free of spiders. spider webs are not helpful
View SolutionAll spiders weave webs, which help them in three things. The webs help the spiders to lay eggs, hide and catch food. Many spiders prefer to lay their eggs in their webs, in which their eggs stay together and secure. The webs are sticky and thus they help the spiders in catching the food. When an insect comes flying in the web, it gets trapped, moves here and there, tries to get out but cannot do so because it is trapped. The spider knows that the insect is trapped because they feel the web move and the spider reaches the insect. Without webs the spider would not be able to live as it does. Spiders need webs to survive, but if you can't find webs in your home, it doesn't mean that your house is free of spiders. Not finding a spider web in the house does not mean that
View SolutionWhich set includes pathogenic arthropods
1. Tse-tse fly, mosquito, flea-plague
2. Crab, Culex, spider
3. Anopheles, culex, cray-fish
4. Silver-fish, housefly, sand-fly
View Solutionक्षैतिज रूप से उड़ रहे एक वायुयान से एक गोले (Bomb) को गिराया जाता है। गोले के मार्ग का आकार होगा
View SolutionMouse is related to Cat in the same way as Fly is related to 1)Animal 2)Horse 3)Spider 4)Rat 5)None of these
View SolutionAll spiders weave webs, which help them in three things. The webs help the spiders to lay eggs, hide and catch food. Many spiders prefer to lay their eggs in their webs, in which their eggs stay together and secure. The webs are sticky and thus they help the spiders in catching the food. When an insect comes flying in the web, it gets trapped, moves here and there, tries to get out but cannot do so because it is trapped. The spider knows that the insect is trapped because they feel the web move and the spider reaches the insect. Without webs the spider would not be able to live as it does. Spiders need webs to survive, but if you can't find webs in your home, it doesn't mean that your house is free of spiders. Here 'to survive' means
View SolutionAll spiders weave webs, which help them in three things. The webs help the spiders to lay eggs, hide and catch food. Many spiders prefer to lay their eggs in their webs, in which their eggs stay together and secure. The webs are sticky and thus they help the spiders in catching the food. When an insect comes flying in the web, it gets trapped, moves here and there, tries to get out but cannot do so because it is trapped. The spider knows that the insect is trapped because they feel the web move and the spider reaches the insect. Without webs the spider would not be able to live as it does. Spiders need webs to survive, but if you can't find webs in your home, it doesn't mean that your house is free of spiders. What is this article mainly about?
View SolutionA glass sphere of refractive index 1.5 has a diameter of 0.2m. A parallel beam is incident on the sphere. Where is it brought to focus by the sphere ?
View SolutionObserve a spider in, its web and write how a spider shares its habitat.
View Solution