A jumper of mass m can slide without friction along parallel horizontal rails separated by a distance d. The rails are connected to a resistor of resistance R and placed in a vertically uniform magnetic field of induction B. The jumper is pushed at a velocity v0 Fig. 106.Determine the distance s covered by the jumper before it comes to rest. How does the direction of induction B affect the answer?
During the motion of the jumper the magnetic flux through the circuit formed by the jumper rails and the resistor changes. An emf is induced in the circuit and a current is generated. As a result of the action of the magnetic field on the current in the jumper the latter will be decelerated.Let us determine the decelerating force F. Let the velocity of the jumper at a certain instant be v. During a short time interval Δt the jumper is shifted along the rails by a small distance Δx = v Δt. The change in the area embraced by the circuit is vd Δt and the magnetic flux varies byduring this time. The emf induced in the circuit isAccording to Ohms law the current through the jumper is I = ξ/R. The force exerted by the magnetic field on the jumper isAccording to Lenzs law the force F is directed against the velocity v of the jumper.Let us now write the equation of motion for the jumper over a small distance Δx:Considering that a = Δv/Δt and v = Δx/Δt we obtainIt can be seen that the change in the velocity of the jumper is proportional to the change in its x-coordinate at the initial instant x0 = 0. Therefore the total change in velocity vf = v0 = 0 - v0 = - v0 is connected with the change in the coordinate with the total displacement s through the relationHence we can determine the length of the path covered by the jumper before it comes to rest:When the direction of the magnetic induction B forms an angle α with the normal to the plane of the rails we obtainIndeed the induced emf and hence the current through the jumper is determined by the magnetic flux through the circuit and in this case the flux is determined by the projection of the magnetic induction B on the normal to the plane of the circuit.
Related Solutions
A jumper of mass m and length l is placed on two prabolic rails in x-y plane. Shape of the rails can be described by Rail 1:y= (and z=0) Rail 2:y= (and z=l) If x is horizontal and y is vertical direction and magnetic field in the space is , the jumper can remain in equilibrium when y coordinate of its ends (i=current in jumper)
View SolutionA conductor of length l and mass m can slide without friction along two vertical rails AB and CD connected by a resistor R. The system is in homogeneous magnetic field of induction B perpendicular to ACBD. How will the movable conductor move in the field of gravity, if the resistance of the conductor itself and the rails are negligible?
View SolutionA pair of parallel conducting rails lie at right angle to a uniform magnetic field of 2.0T as shown in the fig. two resistor 10Omega and 5Omega are to slide without friction along the rail. The distance between the conducting rails is 0.1m . Then
View SolutionA pair of parallel conducting rails lie at right angle to a uniform magnetic field of 2.0T as shown in the fig. two resistor 10Omega and 5Omega are to slide without friction along the rail. The distance between the conducting rails is 0.1m . Then
View SolutionA metal wire of mass m slides without friction on two horizontal rails spaced distance d-apart as shown in figure. The rails are situated in a uniform magnetic field B, directed vertically upwards, and a battery is sending a current I through them. Find the velocity of the wire as a function of time, assuming it to be at rest initially.
View SolutionA metal wire of mass m slides without friction on two horizontal rails spaced at a distance d apart as shown in figure. The rails are situated in a uniform magnetic field B, directed vertically upward, and a battery is sending a current I through them. The velocity of the wire as a function of time is (assuming it to be at rest initially)
View SolutionBefore jumping a long jumper runs a long distance. Indicate the principle of physic, based on which he covers more distance
View Solutionएक कॉपर की छड़ का द्रव्यमान m है। यह दो क्षैतिज समान्तर चिकनी पटरियों (rails) जिनके बीच की दूरी । है तथा क्षैतिज के साथ कोण बनाती है, पर गुरुत्व के अन्तर्गत फिसलती है। तली में पटरियाँ एक प्रतिरोध R के द्वारा चित्रानुसार जुड़ी हैं। यहाँ एकसमान चुम्बकीय क्षेत्र B पटरियों (rails) के तल के लम्बवत् है। छड़ का क्रान्तिक वेग है

View SolutionA wire of length l, mass m and resitance R slides without any friction down the parallel conducting rails of negligible resistance (Fig). The rails are connected to the wire so that the wire and the rails form a closed rectangular conducting loop. The plane of the rails makes an angle theta with the horizontal and a uniform vertical magnetic field of induction B exists throughout the region. Find the steady-state velocity of the wire
View SolutionA long jumper runs before jumping because he
View SolutionA long-jumper runs before jumping because _____.
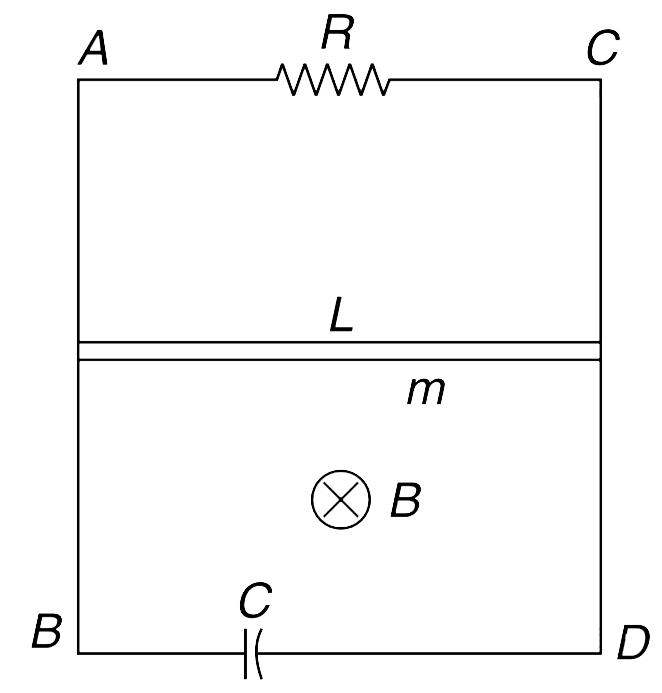
View SolutionTwo long fixed parallel vertical conducting rails AB and CD are separated by a distance L. They are connected by resistance R and a capacitance C at two ends as shown in the figure. There is a uniform magnetic field B directed horizon- tally into the plane of the figure. A horizontal metallic bar of length L and mass m can slide without friction along the rails. The bar is released from rest at t = 0. Neglect resistance of bar and rails and also neglect the self inductance of the loop.
(a) Find the maximum speed acquired by the bar after it is released.
(b) Find the speed of the bar as a function of time t.
View SolutionA copper rod of mass m slides under gravity on two smooth parallel rails l distance apart and set an angle theta to be horizontal. At the bottom, the rails are joined by a resistance R in figure. There is a uniform magnetic field B prependicular to the plane of the rails. The terminal velocity of rod is
View SolutionA wire of length l , mass m and resistance R slides without any friction down the parallel conducting rails of negligible resistance . The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and the rails form a closed rectangualr conducting loop. The plane of the rails makes an angle theta with the horizontal and a uniform vertical magnetic field of the inducetion B exists throughout the rregion. Find the steady state velocity of the wire.
View SolutionA wire of length l , mass m and resistance R slides without any friction down the parallel conducting rails of negligible resistance . The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and the rails form a closed rectangualr conducting loop. The plane of the rails makes an angle theta with the horizontal and a uniform vertical magnetic field of the inducetion B exists throughout the rregion. Find the steady state velocity of the wire.
View SolutionA wire having mass m and length 1 can freely slide on a pair or parallel smooth horizontal rails placed in vertical magnetic field B. The rails are connected by a capacitor of capacitance C . The electric resistance of the rails and the wire is zero .If a constant force F acts on the Wire as shown in the figure . Then ,the acceleration of the wire can be given as

View SolutionTwo parallel resistanceless rails are connected by an inductor of inductance L at one end as shows in Fig. A magnetic field B exists in the space which is perendicular to the plane of the rails. Now a conductor of length l and mass m is placed transverse on the rail and given an inpulse J toward the rightward direction. Then choose the correct option (S).
View SolutionTwo parallel resistanceless rails are connected by an inductor of inductance L at one end as shows in Fig. A magnetic field B exists in the space which is perendicular to the plane of the rails. Now a conductor of length l and mass m is placed transverse on the rail and given an inpulse J toward the rightward direction. Then choose the correct option (S).
View SolutionA metal wire of mass m slides without friction on two rails spaced a distance d apart. The -track lies in a vertical uniform magnetic field of induction B. A constant current i flows from the source as shown. Find the velocity of the wire as a function of time (neglect e=Bdv).
View SolutionA rod of mass m , length l and resistance R is sliding down on a smooth inclined parallel rails with a cinstant velocity v . If a uniform horizontal magnetic field B exists, then find thevalue of B .
View Solution