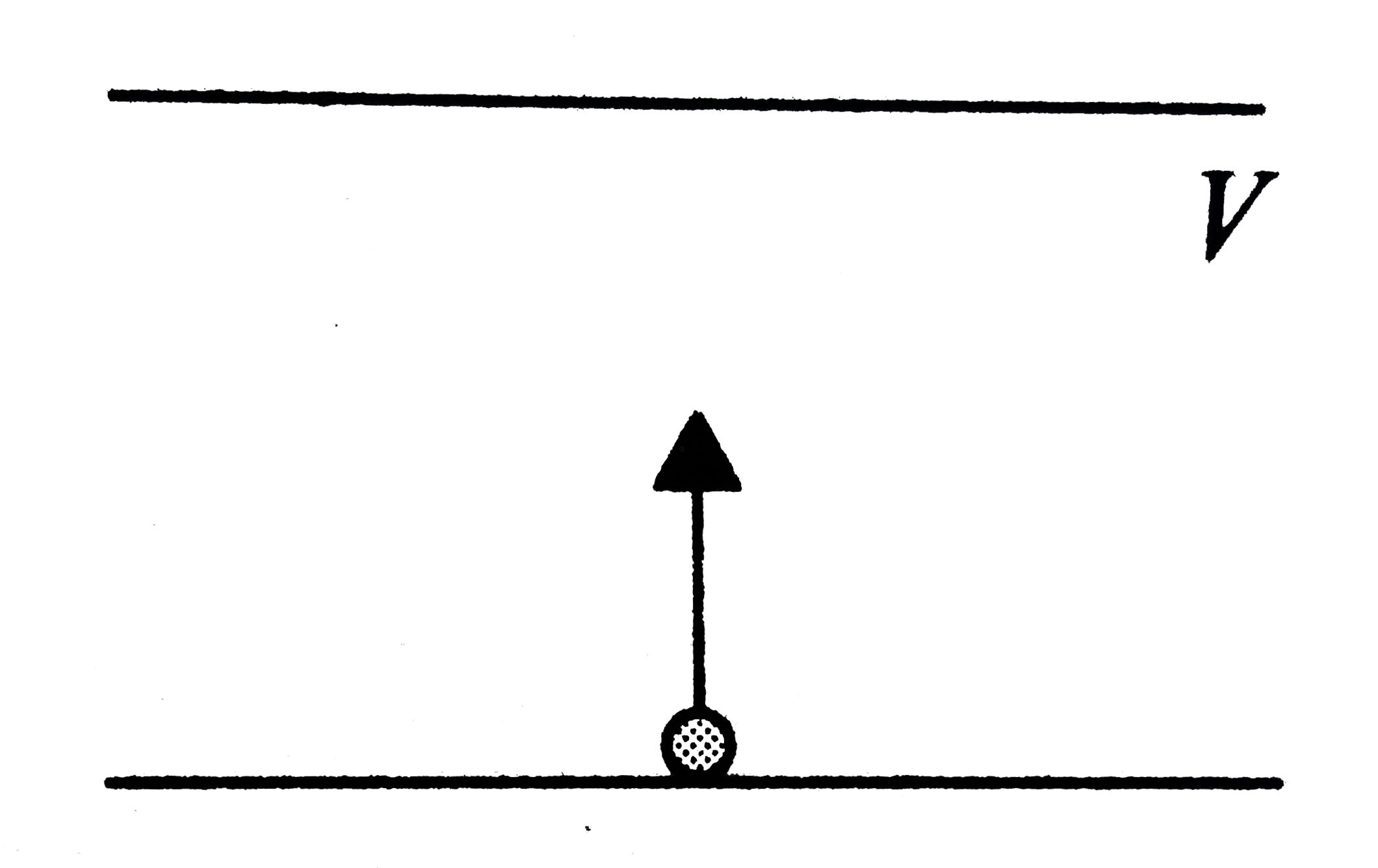
A potential difference V is maintained between two large parallel conducting plates. An electron starts from rest on the surface of one plate and accelerates toward the other. Its speed as it reaches the second plate is proportional toA 1/VB 1/√VC √VD VE V2
The correct option is: C √VExplanation:W = K = qΔV and K = ½ mv2
Related Solutions
Two large conducting plates are placed parallel to each other with a separation of d between them. An electron starting from rest near one of the plates reaches the other plate in time t. If e is the charge on the electron and m is its mass, then the surface charge density on the inner surface is
View SolutionTwo large conducting plates are placed parallel to each other with a separation of 2.00 cm betweeen them. An electron starting from rest near one of the plates reaches the other plate in 2.00 microseconds. Find the surface charge density on the inner surfaces.
View SolutionTwo large conducting plates are placed parallel to each other with a separation of 2.00 cm betweeen them. An electron starting from rest near one of the plates reaches the other plate in 2.00 microseconds. Find the surface charge density on the inner surfaces.
View SolutionTwo large conducting plates are placed parallel to each other with a separation of 2.00 cm betweeen them. An electron starting from rest near one of the plates reaches the other plate in 2.00 microseconds. Find the surface charge density on the inner surfaces.
View SolutionTwo large conducting plates are placed parallel to each other with a separation d . An electron (-e ,m) starting from rest near one of the plates reaches the other plate in time t_(0) . Find the surface density on the inner surface.
View SolutionAn electron having charge and mass starts from the lower plate of two metallic plates separated by a distance . If the potential difference between the plates is , the time taken by the electron to reach the upper plate is given by
 .
.
View SolutionAn electron having charge e and mass m starts from the lower plate of two metallic plates separated by a distance d . If the potential difference between the plates is V , the time taken by the electron to reach the upper plate is given by .
View SolutionThe potential of the plate A of a parallel plate capacitor is zero and the its other plate B is maintained at a potential +V . How does the potential vary from point to point between these plates? Neglect the end effect.
View SolutionA parallel -plate capacitor is connected to a battery that maintains a constant potential difference V between the plates. If the plates are pulled away from each other, increasing their separation, does the magnitude of the charge on the plates (a) increase, (b) decrease, or (c ) remain the same ?
View SolutionThe plates of a parallel plate capacitor are charged to a potential difference of 117 V and then connected across a resistor. The potential difference across the capacitor decreases exponentially with respect to time. After 1 s the potential difference between the plates is 39 V. then after 2 s from the start, the potential difference ( in V) between the plates is
View SolutionThe potential difference between two parallel plates is 10^(4) V. If the plates are separated by 0.5 cm, the force on an electron between the plates is
View SolutionThe distnace between the plates of a parallel plate capacitor is 3 mm the potential difference applied is V. If an electron travels from one plate to another the change in its potential energy is
View SolutionThe distnace between the plates of a parallel plate capacitor is 3 mm the potential difference applied is 3xx10^(5) V. If an electron travels from one plate to another the change in its potential energy is
View SolutionThe potential difference between two large parallel plates is varied as v = at, a is a positive constant and t is time. An electron starts from rest at t=0 from the plate which is at lower potential. If the distance between the plates is L, mass of electron m and charge on electron -e then find the velocity of the electron when it reaches the other plate.
View SolutionThe potential difference between two large parallel plates is varied as v = at, a is a positive constant and t is time. An electron starts from rest at t=0 from the plate which is at lower potential. If the distance between the plates is L, mass of electron m and charge on electron -e then find the velocity of the electron when it reaches the other plate.
View SolutionTwo large parallel conducting plates are separated by 40 mm. The potential difference between the plates is V. Potential difference between points X and Y as indicated in the figure will be
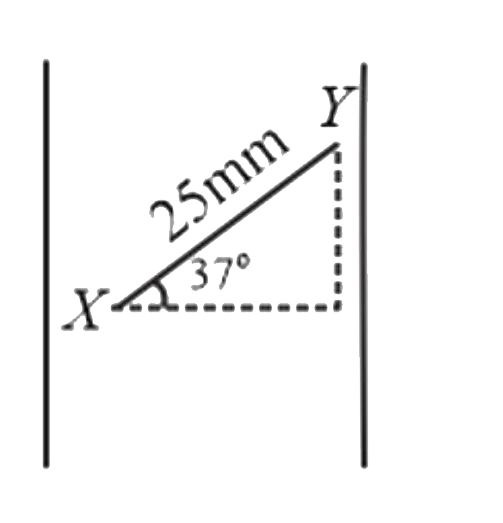
View SolutionTwo large parallel conducting plates are separated by 40 mm. The potential difference between the plates is V. Potential difference between points X and Y as indicated in the figure will be
View SolutionTwo large parallel conducting plates are separated by 40 mm. The potential difference between the plates is V. The potential difference between the points X and Y indicated in the figure will be:
View SolutionThe plates of a parallel plate capacitor are charged to a potential difference of 117 V and then connected across a resistor. The potential difference across the capacitor decreases exponentially with to time.After 1s the potential difference between the plates is 39 V, then after 2s from the start, the potential difference (in V) between the plates is
View SolutionThe plates of a parallel plate capacitor are charged to a potential difference of 117 V and then connected across a resistor. The potential difference across the capacitor decreases exponentially with to time.After 1s the potential difference between the plates is 39 V, then after 2s from the start, the potential difference (in V) between the plates is
View Solution