From the point –1 2 tangent lines are drawn to the parabola y2 = 4 x then the equation of chord of contact isa y = x + 1 b y = x - 1 c y + x = 1 d None of these
Correct option b y = x - 1 Explanation:Chord of contact of -1 2 is yy1 = 2ax + x1 or y = x - 1 .
Related Solutions
Let the midpoint of the chord of contact of tangents drawn from A to the circle be and the points of contact be B and C
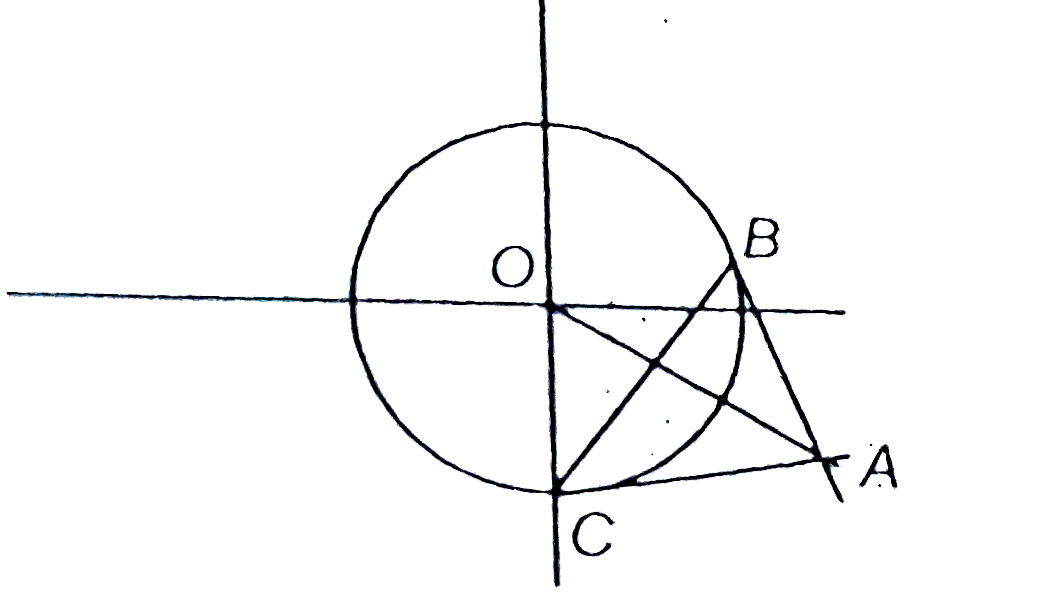
View SolutionLet the midpoint of the chord of contact of tangents drawn from A to the circle be and the points of contact be B and C

View SolutionFrom every point on the line x+y=4 ,tangents are drawn to circle .Then,all chord of contact passes through
View SolutionIf the chord of contact of tangents from a point P to the parabola y^2=4a x touches the parabola x^2=4b y , then the locus of Pdot is a) a cicle b) a parabola c) a straight line d) none of these
View SolutionThe mirror image of the parabola in the tangent to the parabola at the point (1, 2) is (a) (b) (c) (d)
View Solution3.(1) x + y = 0(2) x - y = 0If tangents are drawn from the origin to the curve y = sin x, then their points of contact lie on the curve(3) x2 - y2 = x2y2 (4) x2 + y2 = x2y2(2) x + y = xy(1) X- y = xy
View SolutionIf the line is a tangent to the parabola , then the point of contact is-
View Solutionसिद्ध कीजिए कि रेखा x+y=1 परवलय की स्पर्शी है तथा स्पर्श बिंदु पर अभिलंब का समीकरण y-x+1=0 है अथवा सिद्ध कीजिए कि सरल रेखा x+y=1 परवलय को बिंदु (1,0) पर स्पर्श करती है बिंदु (1,0) पर अभिलंब का भी समीकरण ज्ञात कीजिए
View SolutionThe mirror image of the parabola in the tangent to the parabola at the point (1, 2) is (a) (b) (c) (d)
View SolutionFrom,a point on line y=x+k ,tangents are drawn to (x^(2))/(2)-(y^(2))/(1)=1 such that chords of contact pass through a fixed point (a,b) then (a)/(b)=
View SolutionIf the tangents are drawn from any point on the line to the circle , then the chord of contact passes through the point. (3, 5) (b) (3, 3) (c) (5, 3) (d) none of these
View SolutionThe equation of the tangent to the parabola at the point is
View SolutionTangents are drawn from points of the parabola to the parabola . Find the locus of the mid point of chord of contact.
View SolutionTangents are drawn from any point on the ellipse (x^(2))/(9)+(y^(2))/(4)=1 to the circle x^(2)+y^(2)=1 and respective chord of contact always touches a conic 'C',then- -
View SolutionFind the equation of tangent to the ellipse that perpendicular to the line . Also, find the point of contact .
View SolutionTangents are drawn to the hyperbola (x^(2))/(9)-(y^(2))/(4)=1 parallel to the straight line 2x-y=1 . The points of contact of the tangent on the hyperbola are
View SolutionTangents are drawn to the hyperbol x^2/9-y^2/4=1 ,parallel to the straight line 2x - y = 1 . The points of contacts of the tangents of the hypebola are :
View SolutionFind the equation of tangents drawn to the parabola from the point
View SolutionFind the equation of tangents drawn to the parabola y=x^2-3x+2 from the point (1,-1)dot
View SolutionFind the equation of tangents drawn to the parabola from the point
View Solution