Determine the resistance RAB between points A and B of the frame formed by nine identical wires of resistance R each Fig. 84.
In order to simplify the solution we present the circuit in a more symmetric form Fig. 213. The obtained circuit cannot be simplified by connecting or disconnecting junctions or by removing some conductors so as to obtain parallel or series connected sub-circuits. However any problem involving a direct current has a single solution which we shall try to guess by using the symmetry of the circuit and the similarity of the currents in the circuit.Let us apply a voltage U to the circuit and mark currents through each element of the circuit. We shall require not nine values of current as in the case of arbitrary resistances of circuit elements but only five values I1 I2 I3 I4 and I5 Fig. 214.For such currents Kirchhoffs first rule for the junction Cand for the junction Dwill automatically be observed for the junctions E and F this is due to the equality of the resistances of all resistors of the circuit. Let us now write Kirchhoffs second rule in order to obtain a system of five independent equations:where R is the resistance of each resistor. Solving this system of five equations we shall express all the currents in terms of I1:Considering that the resistance RAB of the circuit satisfies the equation RAB = U/I1 + I2 we obtainTaking into account the relation obtained above we get the following expression for the required resistance:
Related Solutions
A frame is formed by nine identical wires of resistances R each as shown in the figure.
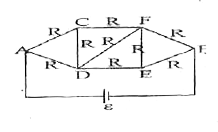
The equivalent resistance between A and B is
View SolutionA frame is formed by nine identical wires of resistances R each as shown in the figure.

The equivalent resistance between A and B is
View SolutionA frame is formed by nine identical wires of resistances R each as shown in the figure. Choose the incorrect statement.
View SolutionA frame is formed by nine identical wires of resistances R each as shown in the figure. Choose the incorrect statement.
View SolutionThe resistance of each side of the square (the smallest one) in the shown wire frame is R. The point is the equivalent resistance of the circuit between A and B.
View SolutionNine resistors each of resistance R are connected in the circuit as shown in fig. The net resistance between A and B is

View SolutionNine resistors each of resistance R are connected in the circuit as shown in fig. The net resistance between A and B is

View SolutionThe network shown in figure is an arrangement of nine identical resistors. The resistance of the network between points A and B is 1.5 Omega . The resistance r is
View SolutionThe network shown in figure is an arrangement of nine identical resistors. The resistance of the network between points A and B is 1.5 Omega . The resistance r is
View SolutionIf the resistance of each edge of a cube shaped wire frame as shown in figure below is R, then the resistance between points 1 and 7 is
View SolutionIn the shown wire frame, each side of a square (the smallest square) has a resistance R. The equivalent resistance of the circuit between the points A and B is

View SolutionIn the shown wire frame, each side of a square (the smallest square) has a resistance R. The equivalent resistance of the circuit between the points A and B is
View SolutionIn the netwrok shown in fig. each resistance is R. The equivalent resistance between A and B is
View SolutionIn the netwrok shown in fig. each resistance is R.

The equivalent resistance between A and B is
View SolutionFind the resistance of a wire frame shaped as cube (Fig) when measured between points (a) 1.7, (b) 1.2, (c) 1.3.
The resitance of each edge of the frame is
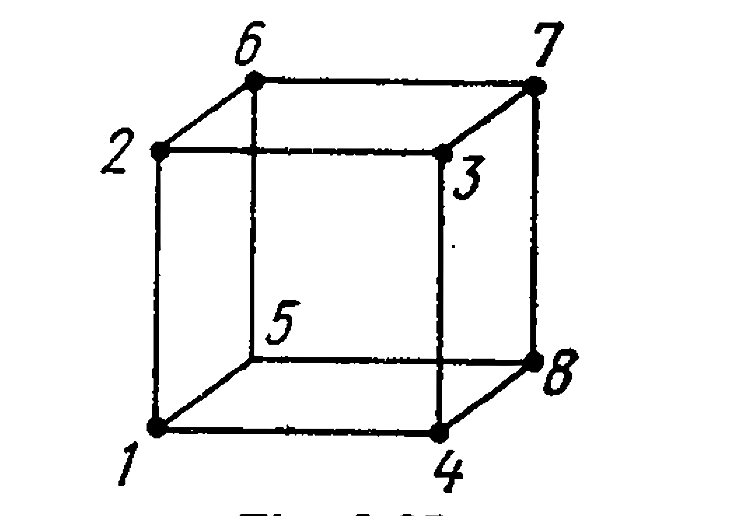
View SolutionFind the resistance of a wire frame shaped as cube (Fig) when measured between points (a) 1.7, (b) 1.2, (c) 1.3.
The resitance of each edge of the frame is

View SolutionFind the equivalent resistance of the circuit shown in Fig.4.60 between the points A and B. Each resistor has a resistance r.

View SolutionIf each resistance r is along 12 sides of a cubical frame of identical wires, then find the equivalent resistance between X and Y, where X and Y are the mean points of two opposite corners of the faces of the cube.
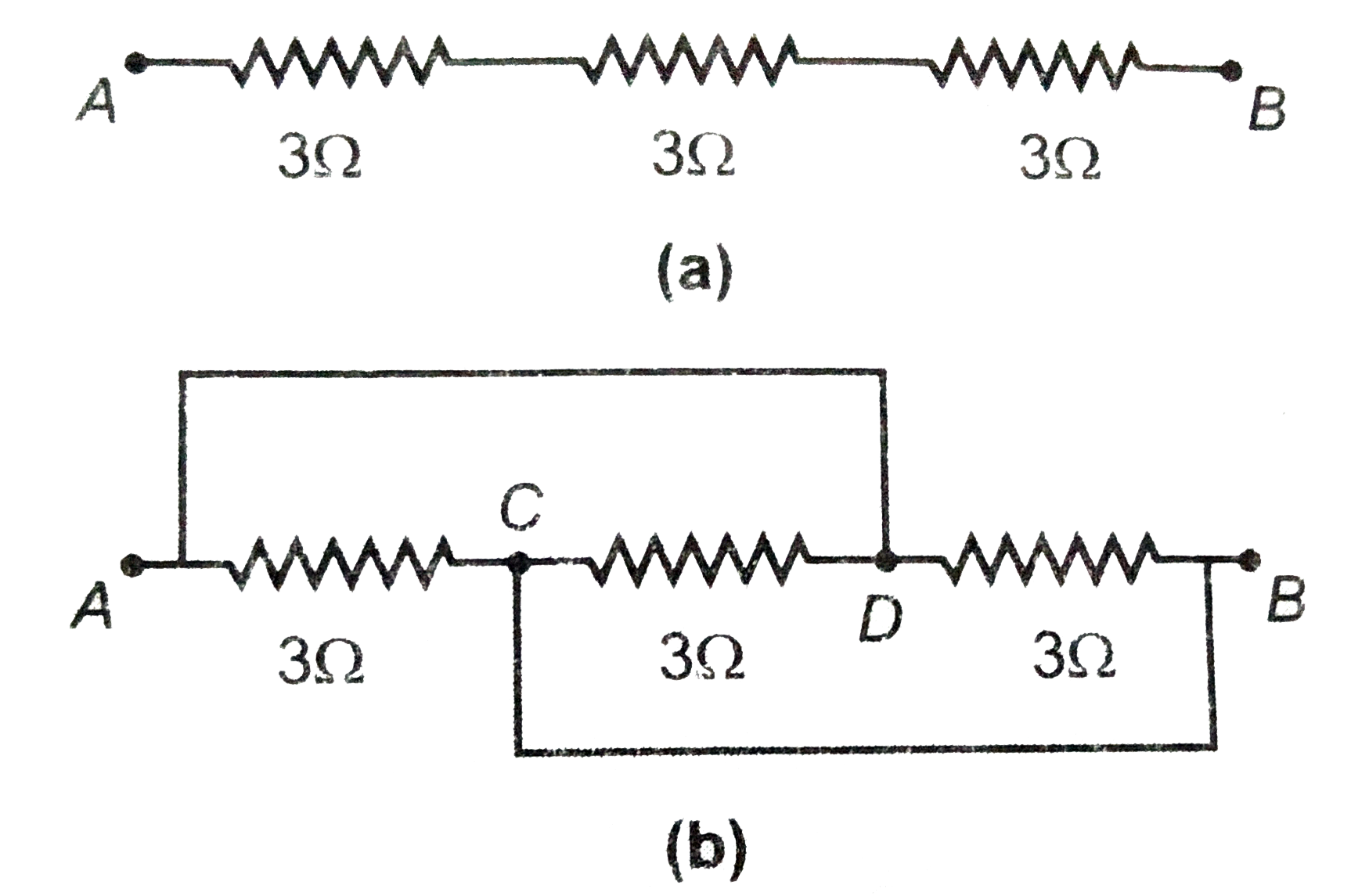
View Solution(A ) चित्र (a) में बिंदु A व B के बीच तुल्य प्रतिरोध ज्ञात कीजिये ।
(B) चित्र (b) में बिंदु A व B के बीच तुल्य प्रतिरोध ज्ञात कीजिये ।
View SolutionTwelve resistors each of resistance are connected in the circuit shown in figure. Net resistance between point A and H would be

View Solution