The properties of a nonlinear resistor were investigated in a series of experiments. At first the temperature dependence of the resistor was studied. As the temperature was raised to T1 = 100°C the resistance changed jump wise from R1 = 50 Ω to R2 = 100 Ω. The reverse abrupt change upon cooling took place at T2 = 99°C. Then a d.c. voltage U1 = 60 V was applied to the resistor. Its temperature was found to be T3 = 80°C. Finally when a d.c. voltage U2 = 80 V was applied to the resistor spontaneous current oscillations were observed in the circuit.The air temperature To in the laboratory was constant and equal to 20°C. The heat transfer from the resistor was proportional to the temperature difference between the resistor and the ambient the heat capacity of the resistor being C = 3 J/K.Determine the period T of current oscillations and the maximum and minimum values of the current.
We denote by a the proportionality factor between the power dissipated in the resistor and the temperature difference between the resistor and the ambient. Since the resistance of the resistor is R1 at T3 = 80°C and the voltage across it is U1 the dissipated power is U12/R1 and we can writeThe temperature of the resistor rises with the applied voltage since the heat liberated by the current increases. As the temperature becomes equal to T1 = 100°C the resistance of the resistor abruptly increases twofold. The heat liberated in it will decrease and if the voltage is not very high the heat removal turns out to be more rapid than the liberation of heat. This leads to a temperature drop to T2 = 99°C which will cause an abrupt change in the resistance to its previous value and the process will be repeated. Therefore current oscillations caused by the jump wise dependence of the resistance on temperature will emerge in the circuit.During these oscillations the temperature of the resistor is nearly constant it varies between T2 = 99°C and T1 = 100°C so that we can assume that the heat removal is constant and the removed power is a T1 - T0. Then by introducing the time t1 of heating from 99°C to 100°C the time t2 of cooling and the oscillation period T = t1 + t2 we can write the heat balance equations:Using the value of a obtained from Eq. 1 we find thatSubstituting the numerical values of the quantities we obtainThe maximum and minimum values of the current can easily be determined since the resistance abruptly changes from R1 = 50 Ω to R2 = 100 Ω in the process of oscillations. Consequently It should be noted that the situation described in the problem corresponds to a first-order phase transition in the material of the resistor. As a result of heating the material goes over to a new phase at T1 = 100°C this transition can be associated for example with the rearrangement of the crystal lattice of the resistor material. The reverse transition occurs at a lower temperature T2 =99°C. This phenomenon is known as hysteresis and is typical of first-order phase transitions.
Related Solutions
When two resistors are connected to a circuit the resultant resistances are .Calculate the value of each resistor.
View SolutionWhat is the effective resistance (in Ω) of two resistors 21 Ω and 28 Ω connected in parallel?
View SolutionIn the circuit shown in fig the voltage across the 2 Ω resistor is 12V. What is the emf of the battery and the current thorugh the 6 Ω resistor?

View SolutionA girl has many resistors of 2 Ω 9 Ω resistance. For this draw a cicuit with the minimum number of resistors.
View SolutionIf are connected in parallel, what will be the current through the resistor?
View Solutionप्रतिरोध तापमापी का 0 डिग्री सेल्सियस पर प्रतिरोध 6 Ω है | 100 डिग्री सेल्सियस पर प्रतिरोध 7 Ω है अज्ञात ताप पर प्रतिरोध का मान 8 Ω है तो अज्ञात ताप की गणना कीजिये |
View SolutionA capacitor of capacitance 2 mF and resistor of resistance 12 Ω are connected in series with voltage source V = (195 sqrt 2 (V))[sin(100 (rad)/s)t] - The average power dissipated in the circuit will be
View SolutionAn inductor of reactance and resistor of resistance are connected in series with a voltage source of emf . The current in the circuit at any time t will be
View SolutionAn inductor of reactance X_L = 4 Ω and resistor of resistance R = 3 Ω are connected in series with a voltage source of emf ε = (20 V)[sin (100pi ((rad)/s))t] . The current in the circuit at any time t will be
View SolutionThree resistors 2 Ω, 3Ω and 4Ω are connected so that the equivalent resistance is 9Ω. The resistors are connected
View SolutionA capacitor of capacitance 2 µF and resistor of resistance 12 Ω are connected in series with voltage source - The average power dissipated in the circuit will be
View SolutionTwo resistors of resistances R1 and R2 in series are connected to a source of emf E . Obtain expressions for potential difference across R1 and R2 .
View SolutionAn inductor of negligible resistance and a 50 Omega resistor are connnected in series across an AC supply of 100 V. Calculate the voltage across the inductor if voltage across the resistor is 40 V.
View SolutionThree resistors of are given in the class.a) What is the highest resistance that you can get using all of them? b) What is the least resistance that you can get using all of them? c) Can you make a resistance using these three? Draw the circuit.
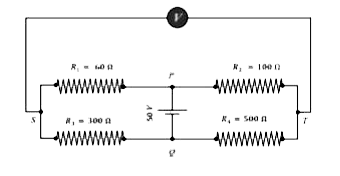
View Solutionसंतुलित अवस्था में एक व्हीटस्टोन सेतु (Wheatstone bridge) की चार भुजाओं के प्रतिरोधक चित्र में दिखाए गए हैं। प्रतिरोधक का ताप गुणांक (temperature coefficient) है । यदि का तापमान बढ़ाया जाता है, तब S और T के बीच उत्पन्न वोल्टता ______ वोल्ट होगी।
View SolutionTwo resistors with temperature coefficients of resistance alpha_1 and alpha_2 have resistances R_(01) and R_(02) at 0^@C . Find the temperature coefficient of the compound resistor consisting of the two resistors connected. a.. In series and b. in paralllel
View SolutionTwo resistors with temperature coefficients of resistance alpha_1 and alpha_2 have resistances R_(01) and R_(02) at 0^@C . Find the temperature coefficient of the compound resistor consisting of the two resistors connected. a.. In series and b. in paralllel
View SolutionResistance of a resistor wire is 5 Omega " at " 50" "^(@)C and 6 Omega " at " 100 " "^(@)C , then its resistance at 0" "^(@) C will be .... .
View SolutionHow many resistors of should be connected in parallel to get 5A current from 230 V supply?
View Solution