A vertical thermally insulated cylinder of volume V contains n moles of an ideal monatomic gas under a weightless piston. A load of mass M is placed on the piston as a result of which the piston is displaced by a distance h.Determine the final temperature Tf of the gas established after the piston has been displaced if the area of the piston is S and the atmospheric pressure is p0.
Since the piston has been displaced by h under the action of the load the volume of the gas has decreased by hS and has become V - hS . The gas pressure under the piston is equal to the atmospheric pressure p0 plus the pressure Mg/S produced by the load i.e. p0 + Mg/S. Therefore we can write the equation of state for the gas before and after loading:Here T1 and Tf are the initial and final temperatures of the gas.Since the gas is thermally insulated by hypothesis it follows from the first law of thermodynamics that the entire work A done on the gas is spent to change its internal energy. i.e. A = 3/2nR Tf - T1 the internal energy of a mole of an ideal gas is U = 3/2RT. It can easily be seen that the work is A = Mgh and hence Subtracting Eq. 1 from Eq. 2 termwise and using expression 3 for Tf - T1 we obtain the following equation in h:Substituting h into Eq. 2 we determine the final temperature of the gas:
Related Solutions
A vertical thermally insulated cylinder of volume V contain n moles of an ideal monoatomic gas under a weightless piston. A load of weight W is placed on the piston as a result of which the piston is displaced. If the initial temp of the gas is 300K , area of piston is A and atmospheric pressure P_(0) . (take W=P_(0)A ). Determine the value of final temperature of the gas
View SolutionA vertical thermally insulated cylinder of volume V contain n moles of an ideal monoatomic gas under a weightless piston. A load of weight W is placed on the piston as a result of which the piston is displaced. If the initial temp of the gas is 300K , area of piston is A and atmospheric pressure P_(0) . (take W=P_(0)A ). Determine the value of final temperature of the gas
View SolutionOne mole of a gas is put under a weightless piston of a vertical cylinder at temperature T. The space over the piston opens into atmosphere. Initially, piston was in equilibrium. How much work should be performed by some external force to increase isothermally the volume under the piston to twice the volume? (Neglect friction of piston).
View SolutionOne mole of a gas is put under a weightless piston of a vertical cylinder at temperature T. The space over the piston opens into atmosphere. Initially, piston was in equilibrium. How much work should be performed by some external force to increase isothermally the volume under the piston to twice the volume? (Neglect friction of piston).
View SolutionOne mole of a gas is put under a weightless piston of a vertical cylinder at temperature T. The space over the piston opens into atmosphere. Initially piston was in equilibrium, How much work should be performed by some external force to increase isothermally the volume under the piston to twice the volume? (Neglect friction of piston)
View SolutionA vertical cylinder of cross-sectional area S contains one mole of an ideal monoatomic gas under a piston of mass M. At a certain instant, a heater that transmits to the gas an amount of heat q per unit time is switched on under the piston. Determine the velocity v of the piston under the condition that the gas pressure under piston is constant and equal to P_0 and the gas under the piston is thermally insulated.
View SolutionA thermally insulated vertical cylinder of cross - section area A contains 3moles of an ideal monatomic gas under a piston of mass M. A heater supplying heat to the gas at constant rate PJ/s, is switched on at t = 0. The velocity of the piston is given by [Take atmospheric pressure as ]
View SolutionThe pressure of a gas contained in a cylinder with a movable piston is 300 Pa. The area of the piston is 0.5 m2. Calculate the force that is exerted on the piston.
View SolutionThe pressure of a gas contained in a cylinder with a movable piston is 300 Pa. The area of the piston is . Calculate the force that is exerted on the piston.
View SolutionOne mole of a gas is put under a weightless piston of a vertical cylinder at temperature T. The space over the piston opens into atmosphere. How much work should be performed by some external force to increase isothermally the volume under the piston to twice the volume (neglect friction of piston)
View Solutionएक सिलेण्डर जिसमे आयतन V तथा दाब P पर एक गैस भरी है, अनुप्रस्थ क्षेत्रफल A का एक पिस्टन लगा है | गैस बॉयल के नियम का पालन करती है | यदि पिस्टन को थोड़ा सा विस्थापित कर दिया जाए, तो कोणीय आकृति क्या है ?
View SolutionTwo moles of an ideal gas are contained in a vertical cylinder with a frictionless piston. The piston is slowly displaced so that expansionin gas is isothermal at temperature K. find the amount of work done in increasing the volume to 3 times.t ake atmospheric pressure
View SolutionTwo moles of an ideal gas are contained in a vertical cylinder with a frictionless piston. The piston is slowly displaced so that expansionin gas is isothermal at temperature T_(0)=400 K. find the amount of work done in increasing the volume to 3 times.t ake atmospheric pressure =10^(5)N//m^(2)
View SolutionAn ideal gas is enclosed in a thermally insulated container. Container is covered by an insulating piston which is connected with spring. Small displacement is given to piston as shown in figure. Which of the following statements is correct? Neglect friction everywhere.
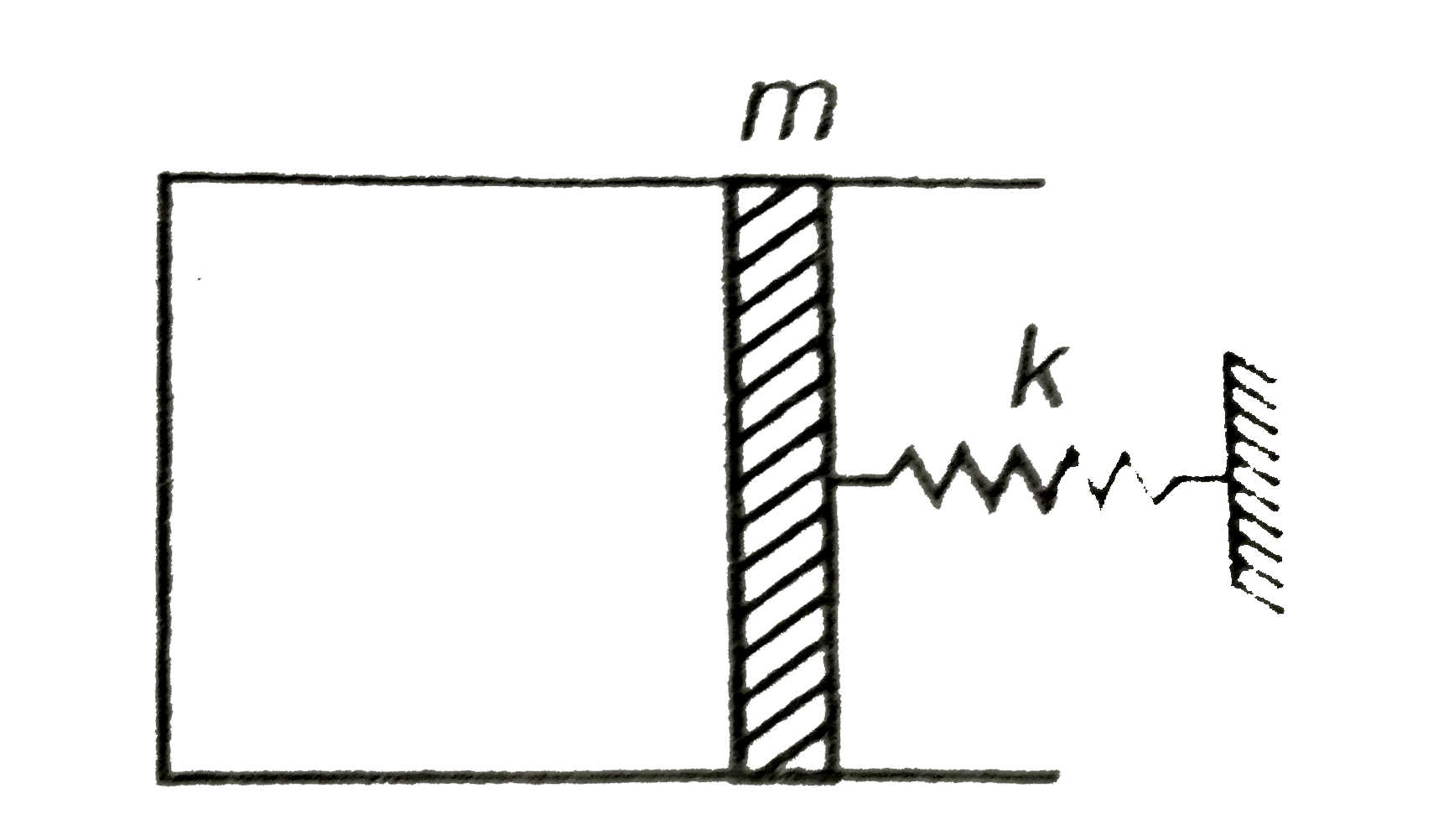
View SolutionAn ideal gas is enclosed in a thermally insulated container. Container is covered by an insulating piston which is connected with spring. Small displacement is given to piston as shown in figure. Which of the following statements is correct? Neglect friction everywhere.
View SolutionA weightless piston divides a thermally insulated cylinder into two parts of volumes and moles of an ideal gas at pressure atmosphere are confined to the part with volume litre. The remainder of the cylinder is evacuated. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy in the process and final temperature of the gas. The ratio of the specific heats of the gas, .
View SolutionA weightless piston divides a thermally insulated cylinder into two parts of volumes and moles of an ideal gas at pressure atmosphere are confined to the part with volume litre. The remainder of the cylinder is evacuated. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy in the process and final temperature of the gas. The ratio of the specific heats of the gas, .
View SolutionA weightless piston divides a thermally insulated cylinder into two parts of volumes and moles of an ideal gas at pressure atmosphere are confined to the part with volume litre. The remainder of the cylinder is evacuated. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy in the process and final temperature of the gas. The ratio of the specific heats of the gas, .
View SolutionA gas is filled in a cylinder fitted with a piston at a definite temperature and pressure. Explain on the basis of kinetic theory why on pulling the piston out, the pressure of decreases.
View SolutionA gas is enclosed in an insulated vessel fitted with insulating piston at a pressure of . On suddenly pressing the piston the volume is reduced to half the initial volume. The final pressure of the gas is
View Solution