A homogeneous aluminium ball of radius r = 0.5 cm is suspended on a weightless thread from an end of a homogeneous rod of mass M = 4.4 g. The rod is placed on the edge of a tumbler with water so that half of the ball is submerged in water whenthe system is in equilibrium Fig. 54. The densities ρal and ρw of aluminium and water are 2.7 x 103 kg/m3 and 1 x 103 kg/m3 respectively.Determine the ratio y/x of the parts of the rod to the brim neglecting the surface tension on the boundaries between the ball and water.
Let x be the length of the part of the rod in the tumbler and y be the length of its outer part. Then the length of the rod is x + y and the centre of mass of the rod is at a distance x + y/2 from its ends and at a distance y - x/2 from the outer end. The condition of equilibrium is the equality to zero of the sum of the moments of force about the brim of the tumbler.where Fb = mbg = ρalgV is the force of gravity of the ball and FA = ρwgV/2 is the buoyant force where V = 4/3πr3 is the volume of the ball. The required ratio is
Related Solutions
A sperical ball of radius r and relative density 0.5 is floating in equilibrium in water with half of it immersed in water. The work done in pushing the ball down so that whole of it is just immersed in water is [ is the density of water]-
View SolutionA spherical ball of radius r and relative density 0.5 is floating in equilibrium in water with half of it immersed in water. The work done in pushing the ball down so that whole of it is just immersed in water is : (where is the density of water)
View SolutionA sperical ball of radius r and relative density 0.5 is floating in equilibrium in water with half of it immersed in water. The work done in pushing the ball down so that whole of it is just immersed in water is [ is the density of water]-
View SolutionA sperical ball of radius r and relative density 0.5 is floating in equilibrium in water with half of it immersed in water. The work done in pushing the ball down so that whole of it is just immersed in water is [ is the density of water]-
View SolutionA spherical ball of radius r and relative density 0.5 is floating in equilibrium in water with half of it immersed in water. The work done in pushing the ball down so that the whole of it is just immersed in water is :
View SolutionA horizontal aluminium rod of diameter 4 cm projected 6 cm from a wall . An object of mass 400 pi kg is suspended from the end of the rod. The shearing modulus of aluminium is 3.0xx10^(10)N//m^(2) . The vertical deflection of the end of the rod is ( :' g = 10 m//s^(2) )
View SolutionA horizontal aluminium rod of diameter 4.8 cm projects 5.3 cm from a wall. A 1200 kg object is suspended from the end of the rod. The shear modulus of aluminium is 3.0xx10^(10)N//m^(2) . Nelecting the mass of te rod find a shearing stress on the rod and b the vertical deflection of the end of the rod.
View SolutionA rubber ball of mass m and radius r is submerged in water to a depth h and released. What height will the ball jump up to above the surface of the water? Neglect ther resistance of water and air. Take water density .
View SolutionA rubber ball of mass 100 g and radius 5 cm is submerged in water to a depth of I m and rele.ised. To what height will the ball jwnp up above the surface of water? (Take g = 10 m s^(-2)
View SolutionA rubber ball of mass 100 g and radius 5 cm is submerged in water to a depth of 1 m and released. To what height will the ball jump up above the surface of water ? (Take g= 10 m s^(-2))
View SolutionAn aluminium rod and a copper rod are taken such that their lengths are same and their resistances are also same. The specific resistance of copper is half that of aluminium, but its density is three timesthat of aluminium. The ratio of the mass of aluminium rod and that of copper rod will be :-
View SolutionWhen a golf ball is lowered into a measuring cylinder containing water, the water level rises by when the ball is completely submerged. If the mass of ball in air is 33 g find its density
View SolutionFigure shows a uniform metal ball suspended by thread of negligible mass from an upright cylinder that floats partially submerged in water. The cylinder has height 6 cm, face area 11 cm2 on the top and bottom and density 0.5 g/. 4 cm of cylinder’s height is inside the water surface. Density of the metal ball is 8gm/. R is the radius of the ball. It is found that where is an integer. Find (system is in equilibrium)
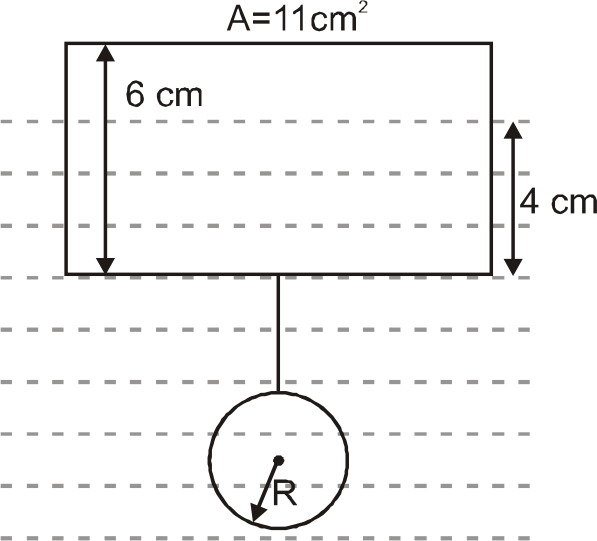
View SolutionFigure shows a uniform metal ball suspended by thread of negligible mass from an upright cylinder that floats partially submerged in water. The cylinder has height 6 cm, face area 11 cm2 on the top and bottom and density 0.5 g/. 4 cm of cylinder’s height is inside the water surface. Density of the metal ball is 8gm/. R is the radius of the ball. It is found that where is an integer. Find (system is in equilibrium)

View SolutionA rubber ball of mass 10 g and radius 2 cm is submerged in water up to a depth of 5 cm and released. Find the height up to which the ball pops up above the surface of water, neglecting the resistance of water and air. The density of water = 1g*cm^(-3) .
View SolutionIn the arrangement shown in fig the mass of the ball 1 is eta=1.8 times as great as that of rod 2 The length of the later is l=100 cm The masses of the pulleys and the threads as well as the friction are negligible The ball is set on the same level as the lower end of the rod and then released How soon will the ball be opposite to the other end of the rod
View SolutionIf 103 cm^(3) of aluminium has a mass of 0.280 kg. Find its density in g//cm^(3)
View SolutionIf 103 cm^(3) of aluminium has a mass of 0.280 kg. Find its density in kg//m^(3)
View SolutionL लम्बाई तथा 1.8 kg द्रव्यमान की समरूप छड़ को इसके दोनों सिरों पर दो मापन स्केल पर विराम में रखा गया है। बांयें सिरे से L/4 दूरी पर 2.7 kg द्रव्यमान का समरूप गुटका छड़ पर रखा जाता है। दांयें सिरे पर मापन स्केल द्वारा अनुभव किया गया बल होगा
View SolutionDensity of aluminium is 2700 kg/ m^(3) . Find the relative density of aluminium given that density of water =10^(3)kg//m^(3)
View Solution