A ray of light propagating in an isotropic medium with refractive index n varying gradually from point to point has a curvature radius ρ determined by the formula where the derivative is taken with respect to the principal normal to the ray. Derive this formula assuming that in such a medium the law of refraction n sin θ = const holds. Here θ is the angle between the ray and the direction of the vector ∇n at a given point.
We consider a ray QPR in a medium of gradually varying refractive index n. At P the gradient of n is a vector with given direction while is nearly the same at neighbouring points Q R. The arc length QR is ds. We apply Snells formula n sin θ = constant where θ is to be measured from the direction vector ∇n. The refractive indices at Q R whose mid point is P are
Related Solutions
A ray of light propagating in an isotropic medium with refractive index varying gradually from point to points has a curvature radius determined by the formula
,
where the derivative is taken with respect to the principle normal to the ray. Derivethis formula, assuming that is such a medium the law of refraction const holds. Here is the angle between the ray and the direction of the vector at a given point.
View SolutionA ray of light passes from vacuum into a medium of refractive index n . If the angle of incidence is twice the angle of refraction , then the relation between the angle of incidence and the refractive index is
View SolutionA ray of light passes from vaccume into a medium of refractive index n. if the angle of incidence is twice the angle of refraction, then the angle of incidence is
View SolutionA ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View SolutionA ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View SolutionIf hati denotes a unit vector along incident light ray, hati a unit vector along refracted ray into medium of refracted ray into medium of refractive index p and n is vector normal to boundary of media directed towards incident medium, then the law of refraction can be written as
View Solutionएकवर्णीय प्रकाश का किरण n अपवर्तनांक के माध्यम में प्रवेश करता है । अपवर्तित किरण की तरंगदैर्घ्य ज्ञात कीजिए ।
View Solutionएकवर्णीय प्रकाश की किरण अपवर्तनांक के माध्यम में प्रवेश करती है|अपवर्तित किरण की तरंग-दैधर्य ज्ञात कीजिये|
View SolutionA ray of light is incident on a medium at an angle i. It is found that the reflected ray is at right angles to the refracted ray . The refractive index of the medium is given by
View SolutionA ray of light is incident on a medium at an angle i. It is found that the reflected ray is right angles to the refracted ray. The refractive index of the medium is given by :
View SolutionA monochromatic ray of light is refracted from vacuum to a medium of refractive index mu . Determine the relation of the wavelengths of light in vacuum and in medium.
View SolutionThe refractive index of a medium with respect to air is . If the angle of incidence of a ray of light in air is determine the angle of deviation for that ray in case of refraction.
View SolutionProceeding from Fermat'sprinciple derive the refraction formula for paraxial rays on a spherical boundary surface of radius between media with refractive indices and .
View SolutionA unit vector along the incident ray of light is . The unit vector for the corresponding refracted ray of light is , a unit vector normal to the boundary of the medium and directed towards the incident medium. If is the refractive index of the medium, then snell's law (second law) of refraction is
View SolutionA unit vector along the incident ray of light is hat(i) . The unit vector for the corresponding refracted ray of light is hat(r ).hat(n) , a unit vector normal to the boundary of the medium and directed towards the incident medium. If mu is the refractive index of the medium, then snell's law (second law) of refraction is
View SolutionThe figure shows the path of ray of light propagating from medium 1 to medium 2. The refractive index of medium 1 with respect to medium 2 is …………………………. .
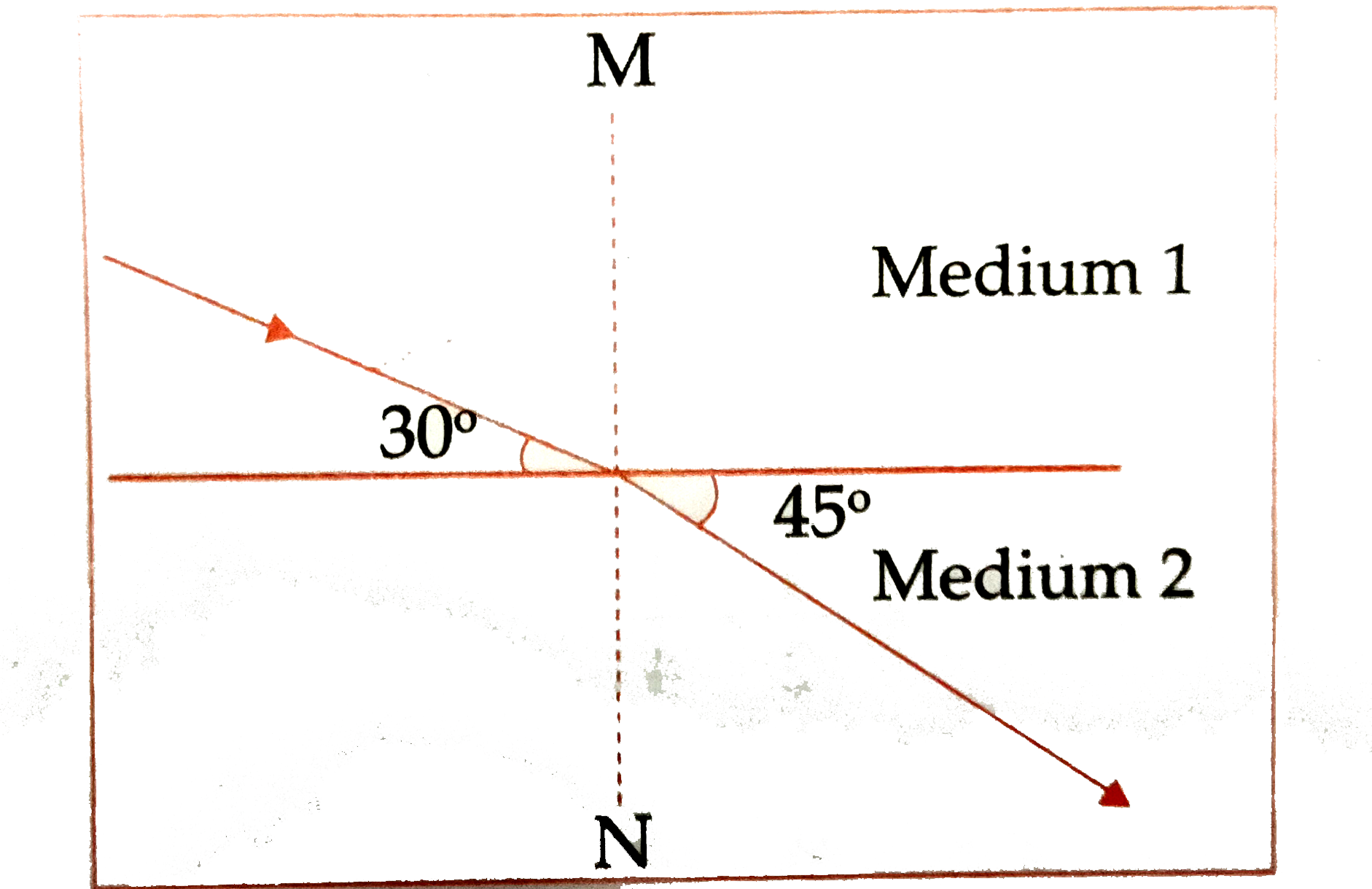
View SolutionThe figure shows the path of ray of light propagating from medium 1 to medium 2.The refractive index of medium 1 with respect to medium 2 is___
View SolutionMonochromatic rays of light coming from vacuum are refracted in a medium of refractive index . Show that the ratio of the wavelength of the incident ray that of the refracted ray is equal to the refractive index of the medium.
View SolutionThe refractive of three media are given below : {:("Medium",A,B,C),("Refractive index",1.65,1.71,1.47):} A light ray travels from medium A to medium B and another light ray travels from medium B to medium C. In which case does (a) the refracted ray bend towards the normal (b) the speed of light will be more.
View SolutionThe refractive of three media are given below :
A light ray travels from medium A to medium B and another light ray travels from medium B to medium C. In which case does (a) the refracted ray bend towards the normal (b) the speed of light will be more.
View Solution