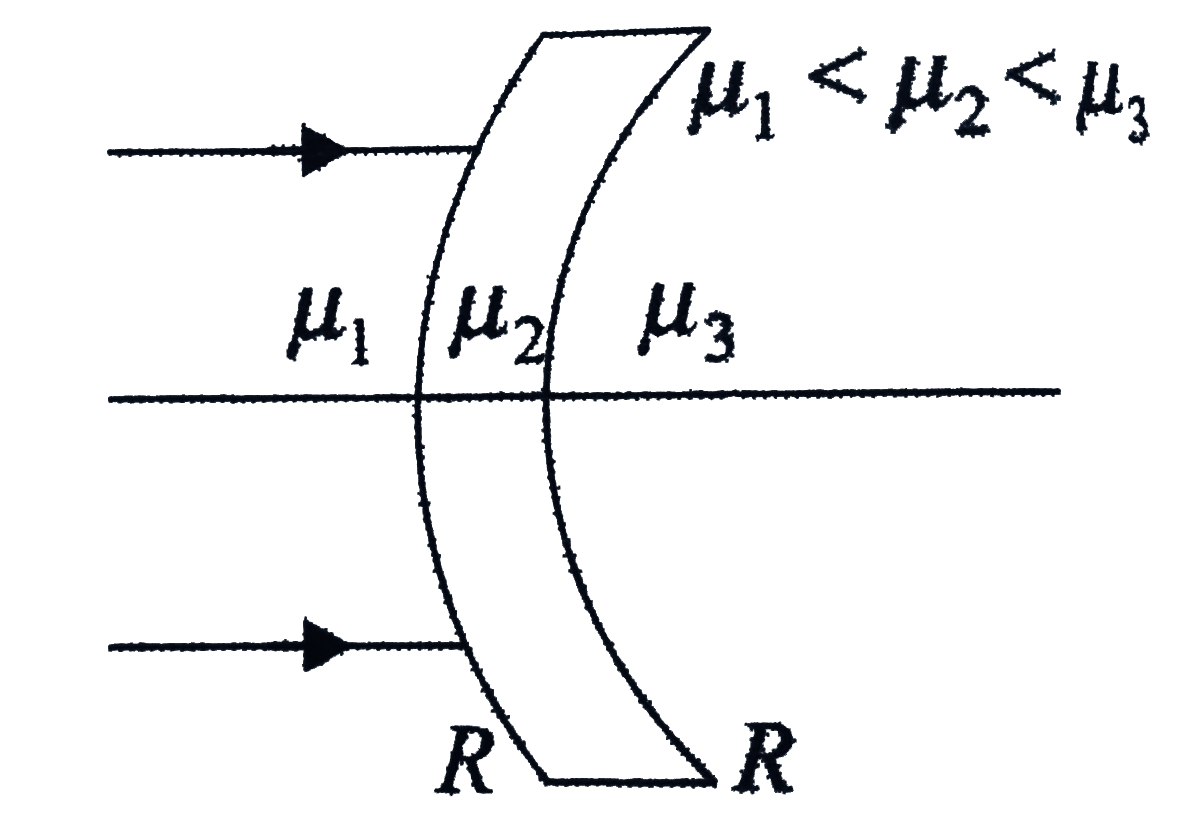
Find the positions of the principal planes the focal length and the sign of the optical power of a thick convex-concave glass lens a whose thickness is equal to d and curvature radii of the surfaces are the same and equal to R; b whose refractive surfaces are concentric and have the curvature radii R1 and R R2 > R1.
a The power of the lens isThe principal planes are located on the side of the convex surface at a distance d from each other with the front principal plane being removed from the con vex surface of the lens by a distance R /n - 1 .Both principal planes pass through the common centre of curvature of the surface of the lens.
Related Solutions
If R1 and R2 are the radii of curvature of a double convex lens. The largest power will be for
View SolutionFind the poistions of the principle planes, the focal length and the sign of the optical power of a thick convex-concave glass lens
(a) whose thickness is equal to and curvature radii of the surfaces are the same and equal to ,
(b) whose refractive surfaces are concentric and have the curvarure radii and .
View SolutionA concave or convex lens is given such that radii of curvature are same. If refractive index of glass is 1.5, then its focal length = ...... where R = radius of curvature.
View SolutionThe radii of curvatures of both surfaces of a double convex lens made of glass, is R. Its focal length is
View SolutionThe radii of curvature of both the surfaces of a lens are equal. If one of the surfaces is made plane by grinding, find the new focal length.
View SolutionA convex lens (with material of refractive index of 3/2) has two surfaces of equal radii of curvature R. The magnitude of its focal length is
View SolutionA convex lens (with material of refractive index of 3/2) has two surfaces of equal radii of curvature R. The magnitude of its focal length is
View SolutionFind the focal length of the lens shown in Fig . The radii of curvature of both the surfaces are equal to R.
View SolutionFind the focal length of the lens shown in the figure. The radii of curvature of both the surfaces are equal to R
View SolutionFind the focal length of the lens shown in Fig . The radii of curvature of both the surfaces are equal to R.
View SolutionThe radii of curvature of both the surfaces of a convex lens are equal. One of the surfaces is made plane by grinding. What is the new focal power of the lens ?
View Solutionकिसी द्वि-उत्तल लेन्स की वक्रता त्रिज्याये समान है। लेन्स के पदार्थ का अपवर्तनांक 1.5 है यदि लेन्स की फोकस दूरी 30 सेमी हो तो उसकी वक्रता त्रिज्याये ज्ञात कीजिये।
View Solutionएक समतल - उत्तल लेन्स के समतल पर चाँदी की परत चढ़ी हुई है। यदि , अपवर्तनांक हो और R , वक्र पृष्ठ का वक्रता व्यासार्ध , तो समूह एक अवतल दर्पण के रूप में व्यवहार करेगा जिसका वक्रता व्यासार्ध है
View SolutionThe radii of curvature of the two surfaces of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5. If the lens is concave -convex, then the focal length of the lens is
View SolutionThe radii of curvature of the two surfaces of a lens are and and the refractive index of the material of the lens is . If the lens is concave convex, then the focal length of lens is
View SolutionThe radii of curvature of the two surfaces of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5. If the lens is concave -convex, then the focal length of the lens is
View SolutionThe radii of curvature of the two surface of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5 . If the lens is concave - convex, then the focal length of the lens is :
View SolutionThe radii of curvature of the two surfaces of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5. If the lens is concave -convex, then the focal length of the lens is
View SolutionCalculate the positions of the principle planes and focal points of a thick convex-concave glass lens if the curvature radius of the convex surface is equal to R_(1) = 10.0 cm and of the concave surface to R_(2) = 5.0 cm and the lens thickness is d = 3.0 cm .
View SolutionThe radii of curvature of both the surfaces of a lens are equal. How will its focal length and power change if one of the surfaces of the lens is made plane ?
View Solution