An electron is located in a unidimensional square potential well with infinitely high walls. The width of the well is l. From the uncertainty principle estimate the force with which the electron possessing the minimum permitted energy acts on the walls of the well.
By uncertainty principle the uncertainty in momentumThe force excerted on the wall can be obtained most simply from
Related Solutions
An electron is located in a unidimensional square potential well with infinitely high walls. The width of the well is . From the uncertainty principle estimate the force with which the electron possessing the minimum permitted energy acts on the walls of the well.
View SolutionA particle is located in a unidimensional square potential well with infinitely high wall. The width of the well is l . Find the normalized wave fucntions of the stationary states of the particle taking the midpoint of the well for the origin of the x coordinate.
View SolutionA particle is in its ground state in a unidimensional potential well with infinitely high walls. Find the force with which the particle acts on the walls. Do the calculations for an electron in a well m wide.
View SolutionA particle is in its ground state in a unidimensional potential well with infinitely high walls. Find the force with which the particle acts on the walls. Do the calculations for an electron in a well 10^(-10) m wide.
View SolutionA particle of mass is located in a unidimensional square potential well with infinitely high walls. The width of the well is equal to . Find the permitted values of energy of the particle taking into accoint that only those states of the particle's motion are realized for which the whole number of de Broglie half waves are fitted within the given well.
View SolutionA electron is located in unidimensional square potential well with infinitely high walls. The width of the well equal to l is such that energy level is very dense. Find the density of the energy levels dN//dE ,i.e., their number per unit energy interval,as a function of E . Calculate dN//dE for E= 1.0 eV if l= 1.0cm .
View SolutionA particle of a mass is located in a two-diamensional square potential well with absolutely impenetrable walls. Find:
(a) the particles permitted energy values if the sides of the well are and
(b) the energy values of the particle at the first four levels if the well has the shape of a square with side .
View SolutionAn electron is confined to a one - dimensional, infinitely deep potential energy well of width L = 100 pm. (a) What is the smallest amount of energy the electron can have? (A trapped electron cannot have zero energy.)
View SolutionDemonstrate that the wave functions of the stationary states of a particle confined in a unidimensional potential well with infinitely high walls are orthogonal i.e., they satisfy the conditions int_(0)^(l)psi_(n)psi_(n),dx=0 if n'!=n . Here l is thewidth of the well , n are integers.
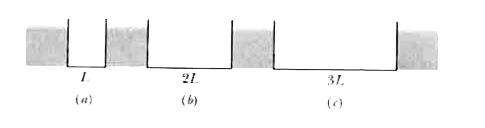
View SolutionThe figure shows three infinite potential wells of widths , each contains an electron in the state for which n = 10. Rank the wells according to (a) the number of maxima for the probability density of the electron and (b) the energy of the electron, greatest first.
View SolutionThe quantum number which specifies the location of an electron as well as energy is
View SolutionEmploying the uncertainty principle, estimate the minimum kinetic energy of an electron confined within a region whose sizes is l=0.20nm .
View SolutionWhat must be the width of a one-dimensional infinite potential well if an electron trapped in it in the n =3 state is to have an energy of 4.7 eV?
View SolutionMaking use of the uncertainty principle,evaluate the minimum permitted energy of an electron in a hydrogen atom and its corresponding apparent distance from the nucleus.
View SolutionConsider an atomic nucleus to be equivalent to a one- dimensional infinite potential well with , a typical nuclear diameter. What would be the ground-state energy of an electron if it were trapped in such a potential well? (Note: Nuclei do not contain electrons.)
View SolutionExplain the term wall pressure exerted by the cell well.
View SolutionDescribe plant cell wall with well labelled diagram.
View SolutionThe group in nitrobenzene:
(i) In resonance act as a electron donating and in inductive effect it act as an electron attracting.
(ii) It acts as an electron donating in resonance as well as inductive effect.
(iii) It acts as an electron attractive in resonance as well as inductive effect.
(iv) It acts as an electron attracting in resonance and electron donating in inductive effect
View SolutionThe group in nitrobenzene:
(i) In resonance act as a electron donating and in inductive effect it act as an electron attracting.
(ii) It acts as an electron donating in resonance as well as inductive effect.
(iii) It acts as an electron attractive in resonance as well as inductive effect.
(iv) It acts as an electron attracting in resonance and electron donating in inductive effect
View SolutionA particle of mass m moves in a unidimensional potential field U= kx^(2)//2 (harmonic oscillator). Using the uncertainty principle, evaluate the minimum permitted energy of the particle in that field.
View Solution