The magnetic induction in a betatron on an equilibrium orbit of radius r varies during the acceleration time at practically constant rate from zero to B. Assuming the initial velocity of the electron to be equal to zero find: a the energy acquired by the electron during the acceleration time; b the corresponding distance covered by the electron if the acceleration time is equal to Δt.
a Even in the relativistic case we know that : p = Berb The distance traversed is
Related Solutions
The magnetic induction in betatron on an equlibrium orbit of radius r varies during the acceleration time at paractically constant rate from zero to B . Assuming the initial velocity of the electron to be equal to zero, find: (a) the energy acquired by the electron during the acceleration time, (b) the corresponding distance covered by the electron if the accelearation time is equal to Delta t .
View SolutionIn a betatron the magnetic flux across an equilibrium orbit of radius grows during the acceleration time at paractically constant rate . In the process, the electrons acquire an energy . Find the number of revolutions made by the electron during the acedeleration time and the corresponding distance covered by it.
View SolutionIn a betatron the magnetic flux across an equilibrium orbit of radius varies during a time interval at practically constant rate from zero to . Find the energy acquired by the electron per revolution.
View SolutionDemonstarate that electrons move in a betatron along a round orbit of constant radius provided the magnetic induction on the orbit of constant radius provided the magnetic induction on the orbit is equal to half the mean value of that indide the orbit (the betatron condition).
View SolutionA body moving in a straight line with constant acceleration covers distances a and b in successive equal time interval of t. The acceleration of the body is
View SolutionA body moving in a straight line with constant acceleration covers distances a and b in successive equal intervals of time t. The acceleration of the body is:
View SolutionA body moving in a straight line with constant acceleration covers distances a and b in successive equal time interval of t. The acceleration of the body is
View SolutionA radius vector of a particle varies with time t as , where a is a constant vector and is a positive factor. Find:
(a) the velocity v and the acceleration w of the particles as functions of time,
(b) the time interval taken by the particle to return to the initial points, and the distance s covered during that time.
View SolutionAn electron initially at rest is accelerated through a p.d. of 1V. The energy acquired by the electron is
View Solutionएक इलेक्ट्रॉन तथा एक प्रोटॉन दोनों को समान विभवान्तर से त्वरित किया जाता है | यदि उनके प्रारंभिक वेग शून्य हों तो इन कणों में -
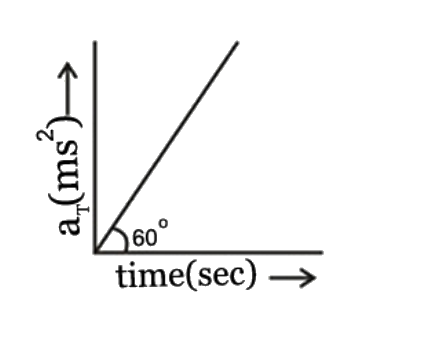
View SolutionTangental acceleration of a particle moving in a circle of radius 1 m varies with time t as shown in figure (initial velocity of the particle is zero). Time after which total acceleration of particle makes an angle of 30^(@) with radial acceleration is
View SolutionAs shown in the figure, the tangential acceleration of a particle moving in a circle of radius 1 m varies with time t (initial velocity of the particle is zero). The time after which the total acceleration of the particle with radial acceleration 30^(@) The angle formed is:
View SolutionTangental acceleration of a particle moving in a circle of radius 1 m varies with time t as shown in figure (initial velocity of the particle is zero). Time after which total acceleration of particle makes an angle of with radial acceleration is
View SolutionA magnetic field of instantaneous induction B is confined to a cylindrical volume of radius R. B is increasing at a constant rate of 0.01 T/s. What is the instantaneous acceleration experienced by an electron placed at a distancer (r ltR) from the centre?
View SolutionThe position "x" of a particle varies with time (t) as x=At^(2)-Bt^(3)" .the acceleration at time t of the particle will be equal to zero
View SolutionThe position x of a particle varies with time t as x=At^(2)-Bt^(3) .the acceleration at time t of the particle will be equal to zero
View SolutionThe position x of a particle varies with time t as .The acceleration of the particle will be zero at time t equal to
View SolutionThe position x of a particle varies with time t as .The acceleration of the particle will be zero at time t equal to
View SolutionThe position x of a particle varies with time t as .The acceleration of the particle will be zero at time t equal to
View SolutionThe position x of a particle varies with time t as . The acceleration of the particle will be zero at time t equal to
View Solution