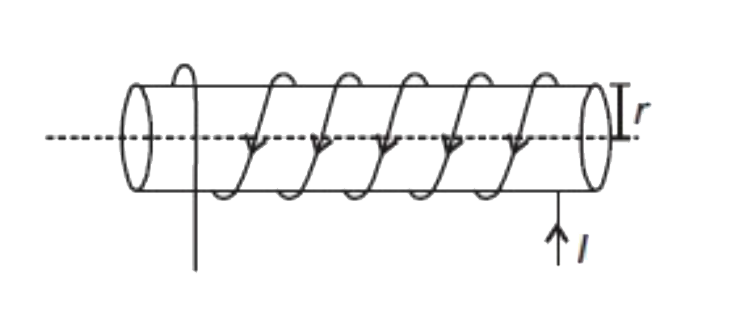
A thin wire ring of radius a and resistance r is located inside a long solenoid so that their axes coincide. The length of the solenoid is equal to l its cross-sectional radius to b. At a certain moment the solenoid was connected to a source of a constant voltage V. The total resistance of the circuit is equal to R. Assuming the inductance of the ring to be negligible find the maximum value of the radial force acting per unit length of the ring.
The solenoid has an inductance where n = number of turns of the solenoid per unit length. When the solenoid is connected to the source an e.m.f. is set up which because of the inductance and resistance rises slowly according to the equationRI + LI = VThis has the well known solution Corresponding to this current an e.m.f. is induced in the ring. Its magnetic field in the solenoid produces a force per unit length acting on each segment of the ring. This force is zero initially and zero for large t. Its maximum value is for some finite t. The maximum value of
Related Solutions
A thin wire ring of radius a and resitance is located inside a long solenoid is equal to , its cross-sectional radius , to . At a certain moment the solenoid was connected to a source of a constant voltage . The total resistance of the circuit is equal to . Assuming the the radial force acting per unit length of the ring.
View SolutionA thin wire ring of radius a and resitance r is located inside a long solenoid is equal to l , its cross-sectional radius , to b . At a certain moment the solenoid was connected to a source of a constant voltage V . The total resistance of the circuit is equal to R . Assuming the the radial force acting per unit length of the ring.
View SolutionThere in fairly long solenoid whose length is l and radial of its cross section is b. This solenoid is connected to a battery of emf V and a, resistor of resistance R in series with it along with a key which is initially open. A thin wire ring of radius a and resistance r is kept inside the solenoid in such a manner that axis of solenoid coincides with axis of ring. Assume thay there in no self-inductance at the ring. Find the value of radical force per unit length of the ring as a function of time if key is closed at t=0. What would be the maximum value of this radical force per unit length?
View SolutionA long solenoid of cross-sectional radius has a thin insulates wiere ring tightly put on its winding, one half of the ring has the resistance times that of the other half. The magneticv induction produced by the solenoid varies with the time as , where is a constant. Find the magnitude of the electric field strength in the ring.
View SolutionA long solenoid of cross-sectional radius a has a thin insulates wiere ring tightly put on its winding, one half of the ring has the resistance eta times that of the other half. The magneticv induction produced by the solenoid varies with the time as B = bt , where b is a constant. Find the magnitude of the electric field strength in the ring.
View SolutionA wire of fixed length is wound on a solenoid of length l and radius r, its self inductance is found to be L. If same wire is wound on a solenoid of length and radius , then self inductance will be
View SolutionA wire of fixed length is wound on a solenoid of length l and radius r . Its self-inductance is found to be L . Now, if the same wire is wound on a solenoid of length l//2 and radius r//2 then the self-inductance will be
View SolutionMass m of a material of density d and resistivity p is used to make a solenoid of length l. Total resistance of the wire is R. Self-inductance of the solenoid is
View SolutionA long narrow solenoid of radius a has n turns per unit length and resistance of the wire wrapped on it is R. The solenoid is connected to a battery of emf V through a variable resistance R_(x) . There is a conducting ring of radius 2a held fixed around the solenoid with its axis coinciding with that of the solenoid. The relaxation time of free electrons inside the material of the conducting ring at given temperature is tau and specific charge of an electron is alpha . The variable resistance R_(x) is changed linearly with time from zero to R in an interval Delta t . Calculate the drift speed of the free electrons in the ring during this interval. [Neglect inductance]
View SolutionThe diagram shows a solenoid carrying time varying current ( is constant) on the axis of this solenoid a conducting ring is being placed as shown in the figure. The mutual inductance of the ring and the solenoid is M and self inductance of the ring is L . if the resistance of the ring is R then the maximum current which can flow through the ring is
View SolutionCalculate the inductance of a closely wound solenoid of length l whose winding is made of copper wire of mass m. The winding has a total resistance equal to R. The solenoid diameter is considerably less than its length. .
View SolutionThe diagram given below shows a solenoid carrying time varying current l= l_(0)t . On the axis of the solenoid, a ring has been placed. The mutual inductance of the ring and the solenoid is M and the self inductance of the ring is L. If the resistance of the ring is R then maximum current which can flow through the ring is
View SolutionThe diagram given below shows a solenoid carrying time varying current l= l_(0)t . On the axis of the solenoid, a ring has been placed. The mutual inductance of the ring and the solenoid is M and the self inductance of the ring is L. If the resistance of the ring is R then maximum current which can flow through the ring is
View SolutionA long one layer solenoid tightly would of wire with resistivity has turns per unit length. The thickness of the wire insulation is negligible. The cross sectional radius of the solenoid is equal to . Find the phase difference between current and alternating voltage fed to the solenoid with frequency .
View SolutionOn a long solenoid of cross-section radius R, a thin non-conducting wire ring of uniform cross-section is mounted tightly to its winding. A ring is made of two different materials in such a way that the resistance of one half of the ring is 10 times that of the other half. The magnetic induction produced by the solenoid varies with time as B = bt, where . is a constant. What is the magnitude of the electric field strength (other than the induced electric field) in the ring?
View SolutionFind the inductance of a solenoid of length whose winding is made of copper wire of mass . The winding resistance is equal to . The solenoid diameter is considerably less than its length.
View SolutionFor a solenoid keeping the turn density constant its length makes halved and its cross section radius is doubled then the inductance of the solenoid increased by :-
View SolutionThe magnetic field within a long, straight solenoid with a circular cross - section of radius r is (as shown) increasing at a rate of alpha . The rate of change of flux through a circle with radius a inside the solenoid and with centre on the solenoid axis is
View SolutionThe magnetic field within a long, straight solenoid with a circular cross - section of radius r is (as shown) increasing at a rate of .
The rate of change of flux through a circle with radius a inside the solenoid and with centre on the solenoid axis is
View SolutionA solenoid of radius 2.50cm has 400turns and a length of 20.0cm. The inductance (L) of this solenoid is ________.
View Solution