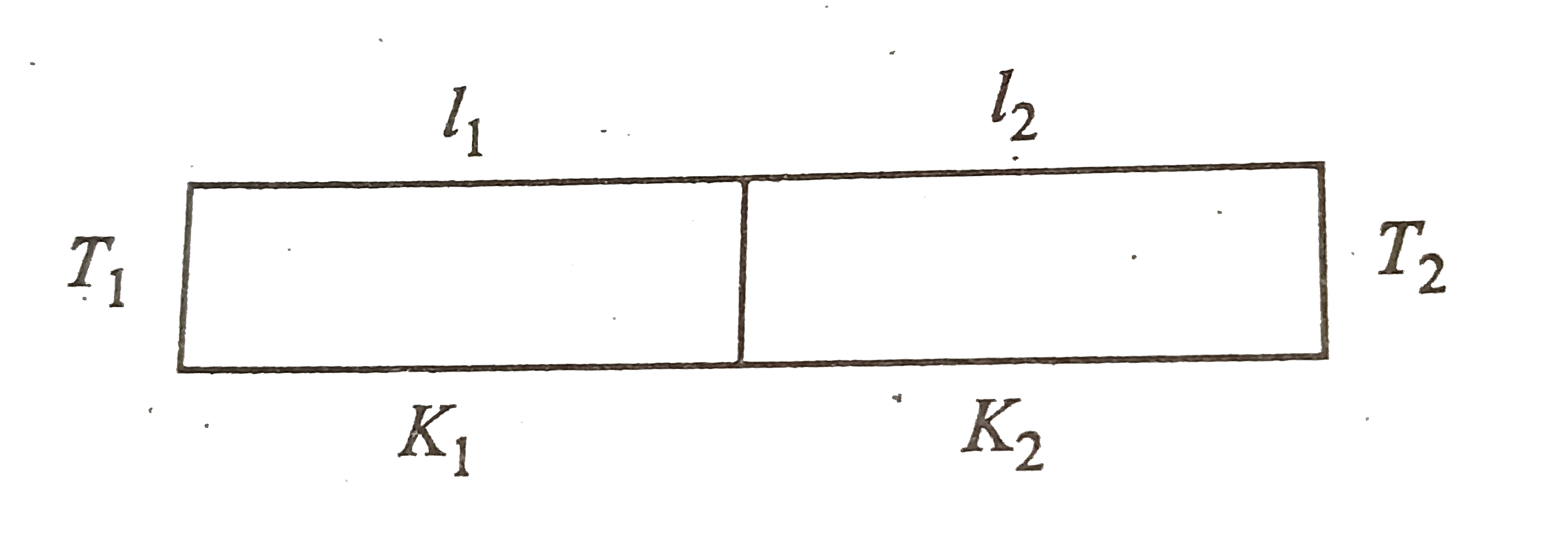
One end of a rod enclosed in a thermally insulating sheath is kept at a temperature T1 while the other at T2. The rod is composed of two sections whose lengths are l1 and l2 and heat conductivity coefficients x1 and x2. Find the temperature of the interface.
Let T = temperature of the interface. Then heat flowing from left = heat flowing into right in equilibrium.
Related Solutions
One end of a rod, enclosed in a thermally insulating sheath, is kept at a temperature while the other, at . The rod is composed of two sections whose lengths are and and heat conductivity coefficients and . Find the temperature of the interface.
View SolutionOne end of a thermally insulated rod is kept at a temperature T_1 and the other at T_2 . The rod is composed of two sections of length l_1 and l_2 and thermal conductivities K_1 and K_2 respectively. The temperature at the interface of the two section is
View SolutionOne end of a thermally insulated rod is kept at a temperature T_1 and the other at T_2 . The rod is composed of two sections of length l_1 and l_2 and thermal conductivities K_1 and K_2 respectively. The temperature at the interface of the two section is
View Solutionone end of an insulating rod T_1 on heat and T_2 is kept on heat. rods respectively l_1 And l_2 lengths and thermal conductivity K_1 And K_2 made up of two parts. The temperature at the interface of the two parts is
View SolutionOne end of thermally insulated rod is kept at a temperature T_(1) and the other at T_(2) . The rod is composed of two section of length l_(1) and l_(2) thermal conductivities k_(1) and k_(2) respectively. The temerature at the interface of two section is
View SolutionOne end of thermally insulated rod is kept at a temperature T_(1) and the other at T_(2) . The rod is composed of two section of length l_(1) and l_(2) thermal conductivities k_(1) and k_(2) respectively. The temerature at the interface of two section is
View SolutionOne end of thermally insulated rod is kept at a temperature T_(1) and the other at T_(2) . The rod is composed of two section of length l_(1) and l_(2) thermal conductivities k_(1) and k_(2) respectively. The temerature at the interface of two section is
View SolutionOne end of thermally insulated rod is kept at a temperature and the other at . The rod is composed of two section of length and thermal conductivities and respectively. The temerature at the interface of two section is
View SolutionTwo rods whose lengths are l_1 and l_2 and heat conductivity coefficient x_1 and x_2 are placed end to end. Find the heat conductivity coefficient of a uniform rod of length l_1 + l_2 whose conductivity is the same as that of the system of these two rods. The lateral surfaces of the rods are assumed to be thermally insulated.
View SolutionA rod of length l with thermally insulated lateral surface consists of material whose heat conductivity coefficient varies with temperature as , where a is a constant. The ends of the rod are kept at temperatures . Find the function T(x), where x is the distance from the end whose temperature is .
View SolutionA rod of length l with thermally insulated lateral surface consists of material whose heat conductivity coefficient varies with temperature as k= a//T , where a is a constant. The ends of the rod are kept at temperatures T_1 and T_2 . Find the function T(x), where x is the distance from the end whose temperature is T_1 .
View Solutionone end of an insulating rod T_(1) on heat and the other end T_(2) is kept on heat. rods respectively I_(1) And I_(2) lengths and K_(1) And K_(2) The thermal conductivity is made up of two parts. The temperature at the interface of the two parts is:
View Solutionएक ऊष्मीय रुद्ध छड़ का एक सिरा ताप पर तथा दूसरा सिरा ताप पर रखा जाता है | छड़ चित्र की भाँतिदो खंडो से बनी है , जिसकी लंबाइयाँ व तथा ऊष्मा चालकताएँ क्रमशः व है | दोनों खंडो के अंतरापृष्ठ का ताप होगा -
View SolutionThe thermal conductivity coefficients of the two metal bars of length x1 and x2 and cross section are k1 and k2 respectively.
View SolutionA rod of length l with thermally insulated lateral surface, end area A consists of a material whose thermal conductivity varies with temperature as where , a and b are containts. and () are temperature of two ends of rod. Then rate of flow of heat across the rod is
View SolutionA rod of length // with thermally insulated lateral surface of area A consists of a material whose heat conduction co-efficient varies with temperature as k = k_0/(a+bT) The two ends of the rod are temperatures T_1 and T_2 (ltT_1) Find the heat transferred across the rod.
View SolutionA rod of lengh l with thermally insulated lateral surface consists of material whose heat conductivity coefficient varies with temperature as x=alpha//T , where alpha is a constant. The end of the rod are kept at temperature T_(1) and T_(2) . Find the heat flow density.
View Solution0.5 मीटर लम्बी एक छड़ की ताप प्रणवता प्रति मीटर है | यदि छड़ के तप्त सिरे का ताप है, तो उसके दूसरे सिरे का ताप बताइयें |
View SolutionA rod of length with thermally insulated lateral surface of area A consists of a material whose heat conduction co-efficient varies with temperature as The two ends of the rod are temperatures and
Express the temperature of the rod at a points as a function of, x, distance from the hot end.
View Solution40 सेमी लम्बी एक छड़ A के सिरों का तापान्तर तथा 60 सेमी लम्बी दूसरी छड़ B के सिरों का तापान्तर है। दोनों छड़ें परस्पर बराबर अनुप्रस्थ काट की हैं। यदि दोनों छड़ों में ऊष्मा चालन की दरें भी बराबर हों, तो छड़ों के पदार्थों के ऊष्मा चालकता गुणांकों का अनुपात ज्ञात कीजिए।
View Solution