Find the law according to which the mass of the rocket varies with time when the rocket moves with a constant acceleration w the external forces are absent the gas escapes with a constant velocity u relative to the rocket and its mass at the initial moment equals m0.
According to the question vector Fexternal force=0
Related Solutions
Find the law according to which the mass of the rocket varies with time, when the rocket moves with a constant acceleration w, the external forces are absent, the gas escapes with a constant velocity u relative to the rocket, and its mass at the initial moment equals .
View SolutionA rocket is moving with constant acceleration . Assume external forces on it to be zero . Exhaust gases escape with velocity u relative to the rocket . Find how its mass changes with time if its initial mass is .
View SolutionFind the mass of the rocket as a function of time, if it moves with a constant acceleration , in absence of external forces. The gas escapes with a constant velocity relative to the rocket and its mass initially was .
View SolutionFind the mass of a rocket as function of time , it it moves with a constant acceleration alpha in te absence of external forces. The gas escape with a constant velocity u relative to the rocket and its mass initially was m_(0)
View SolutionFind the mass of the rocket as a function of time, if it moves with a constant acceleration , in absence of external forces. The gas escapes with a constant velocity relative to the rocket and its mass initially was .
View SolutionA rocket is moving with constant acceleration 6. Assume external forces on it to be zero. Exhaust gases escape with velocity u relative to the rocket. Find how its mass changes with time if its initial mass is .
View SolutionA rocket is moving with constant acceleration 6. Assume external forces on it to be zero. Exhaust gases escape with velocity u relative to the rocket. Find how its mass changes with time if its initial mass is .
View SolutionA rocket moves in the absence of external forces by ejecting a steady jet with velocity u constant relative to the rocket. Find the velocity v of the rocket at the moment when its mass is equal to m, if at the initial moment it possessed the mass m_0 and its velocity was equal to zero. Make use of the formula given in the foregoing problem.
View SolutionA relativistic rocket emits a gas jet with non-relativistic velocity u constant relative to the rocket. Find how the velocity v of the rocket depends on its rest mass m if the initial rest mass of the rocket equals to m_0 .
View SolutionA rocket ejects a steady jet whose velocity is equal to u relative to the rocket. The gas discharge rate equals mu kg//s . Demonstrate that the rocket motion equation in this case takes the form mw=F-muu , where m is the mass of the rocket at a given moment, w is its acceleration, and F is the external force.
View SolutionA rocket with an initial mass is going up with a constant acceleration a by exhausting gases with a velocity v relative to the rocket motion, then the mass of the rocket at any instant of time is (assume that no other forces act on it)
View SolutionIf M is the mass of the rocket, r is the rate of release of gases relative to the rocket, then the acceleration of the rocket (dv)/(dt) (Gases move relative to rockets = u)
View SolutionA double stage rocket has an initial mass M_(1) . Gas is exhausted from the rocket at a constant rate of dm/dt and with an exhaust velocity u relative to the rocket. When the mass of the rocket reaches the value 'mu' the first state of mass m is disengaged from the rocket then the rocket continues the second stage at the same rate (dm/dt) and exhaust velocity (u) as in the first stage unit it reaches a mass M_(f) . If gravity is neglected and the rocket has started from rest, the velocity of the rocket at the end of first stage is
View SolutionThe rate of mass of the gas emitted from the rear of a rocket is initially . If the speed of the gas relative to the rocket is and the mass of the rocket is , then the acceleration of the rocket in is
View SolutionA rocket moves, in the absence of external forces, acceleration depends upon time 't' as a = Kt where k is a positive constant. Derive an expression, for the mass 'm' of the rocket at any instant, if its initial mass be m_(0) and the exhaust escape with a constant velocity 'u' relative to the rocket is m = m_(0) e^(-(k t^(2))/(x u)) where 'x' is
View SolutionA rocket with initial mass M is launched by emitting, gas wil velocity (relative to the rocket body) downwards. The mass of the gas emitted per seconds is k. (k is constant and obeys ). Find time when rocket start to lift.
View SolutionA rocket consumes 24kg of fuel per second The burnt gases escape the rocket at a speed of 6.4km//s relative to the rocket Calculate the upthrust recevied by the rocket Also calculate the velocity acquired by the rocket when the mass redues to 1//100th of its initial mass.
View SolutionIn case of rocket propulsion, choose the correct options. a) momentum of rocket always remains constant. b) Newton's third law is applied. c) If exhaust velocity and rate of burning of mass is kept constant, then acceleration of rocket will go on increasing. d) If exhaust velocity and rate of burning of mass is kept constant, then thrust force will be constant.
View SolutionThe mass rate of gases released from the back of the rocket is primarily 0.1 kg/ sec Huh. If the gas moves relative to the rocket 50m/sec And the mass of the rocket 2 kg, then the acceleration of the rocket m/sec^(2) Will be in
View SolutionIf rocket engine ejects fuel at the rate kg/s with relative velocity . At time t = 0, speed of rocket is u. Consider the value of acceleration due to gravity is constant and equal to g.
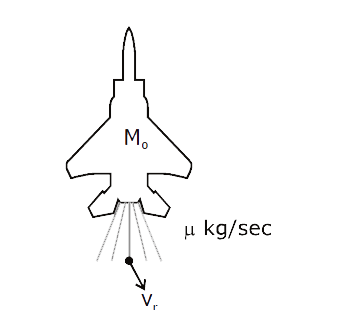
If rocket is in gravity free space then find velocity of rocket as function of time.
View Solution