An ideal gas of molar mass /If is located in the uniform gravitational field in which the free-fall acceleration is equal to g. Find the gas pressure as a function of height h if p = P0 at h = 0 and the temperature varies with height asa T = T0 1 - ah; b T = T0 1+ ah where a is a positive constant.
We known that the variation of pressure with height of a fluid is given by :b Proceed up to Eq. 1 of part a and then put T = T01+ah in the same fashion to get
Related Solutions
An ideal gas of molar mass is located in the uniform gravitational field in which the free-fall acceleration is equal to . Find the gas pressure as a function of height . If at , and the temperature varies with height as
(a) ,
(b) ,
where is a positive constant.
View SolutionAn ideal gas of molecular mass M is located in the uniform gravitational field in which the free-fall acceleration is g. Find the gas pressure as a function of height h, if P is equal at h = 0 and the temperature varies with has (1-ah). where a is a positive constant.
View SolutionAn ideal gas of molar mass is contained in a very tall vertical cylindrical vessel in the uniform gravitational field in which the free-fall acceleration equals to , find the height at which the centre of gravity of the gas is located.
View SolutionAn ideal gas of molar mass contained in a very tall vertical cylindrical column in the uniform gravitational field. Assuming the gas temperature to be T, the height at which the centre of gravity of the gas is located is (R: universal gas constant)
View SolutionAn ideal gas of molar mass M is contained in a tall vertical cylindrical vessel whose base area is S and height h . The temperatuer of the gas is T , its pressure on the bottom bass is p_0 . Assuming the temperature and the free-fall acceleration g to be independent of the height, find the mass of gas in the vessel.
View SolutionThe velocity of a body falling freely under gravitational field varies as g^(p)h^(q) , where g is gravitational acceleration and h is height from which the body is released. p and q are given by
View SolutionAn ideal gas is expanding such that constant. The coefficient of volume expansion of the gas is , where is temperature in Kelvin and is pressure, Find the value of A.
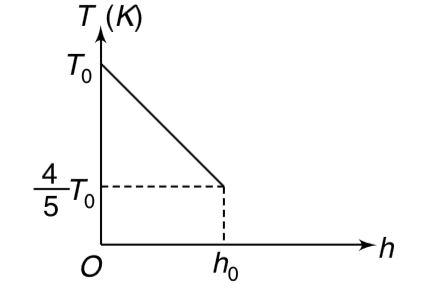
View Solution(a) Assume the atmosphere as an ideal gas in static equilibrium at constant temperature T0. The pressure on the ground surface is P0. The molar mass of the atmosphere is M. Calculate the atmospheric pressure at height h above the ground.
(b) To be more realistic, let as assume that the temperature in the troposphere (lower part of the atmosphere) decreases with height as shown in the figure. Now calculate the atmospheric pressure at a height h0 above the ground.
View SolutionShow that the volume coefficient of on ideal gas at constant pressure equals T^(-1) where T is the absolute temperature
View SolutionA tall cylindrical vessel with gaseous nitrogen is located in a uniform gravitational field in which the free-fall acceleration is equal to . The temperature of the nitrogen varies along the height so that its density is the same throught the volume. find the temperature gradient .
View SolutionIf P,T, p and R represent pressure, temperature, density and universal gas constant respectively then the molar mass of the ideal gas is given by
View SolutionIf P, V, M, T and R are symbols of pressure, volume, molecular weight, temperature and Gas contstant, what is the equation of density of ideal gas
View Solutionयदि तथा R क्रमशः दाब, आयतन मोलर द्रव्यमान, ताप तथा गैस स्थिरांक है तो एक आदर्श गैस का घनत्व होगा :
View SolutionThe temperature of n moles of an ideal gas is increased from T to 4T through a process for which pressure where a is a constant .Then the work done by the gas is
View SolutionThe temperature of n moles of an ideal gas is increased from T to 4T through a process for which pressure P = aT^(-1) where a is a constant. Then, the work done by the gas is
View Solutionकिसी आदर्श गैस के 1 लीटर में मोलो की संख्या क्या होगी यदि इसका दाब P, गैस नियतांक R तथा ताप T है ?
View SolutionIf P, V,M, T and R are pressure, volume, molar mass, temperature and gas constant respectively, then for an ideal gas, the density is given by
View SolutionIf P, V,M, T and R are pressure, volume, molar mass, temperature and gas constant respectively, then for an ideal gas, the density is given by
View SolutionIf P,V,M,T and R are pressure, volume, molar mass, temperature and gas constant respectively, then for an ideal gas, the density is given by .
View SolutionA vessel contains 1 mole of 0, gas (molar mass ) at a temperature . The pressure of the gas is . An identical vessel containing one mole of He gas (molar mass = 4) at a temperature , has a pressure of . Find .
View Solution