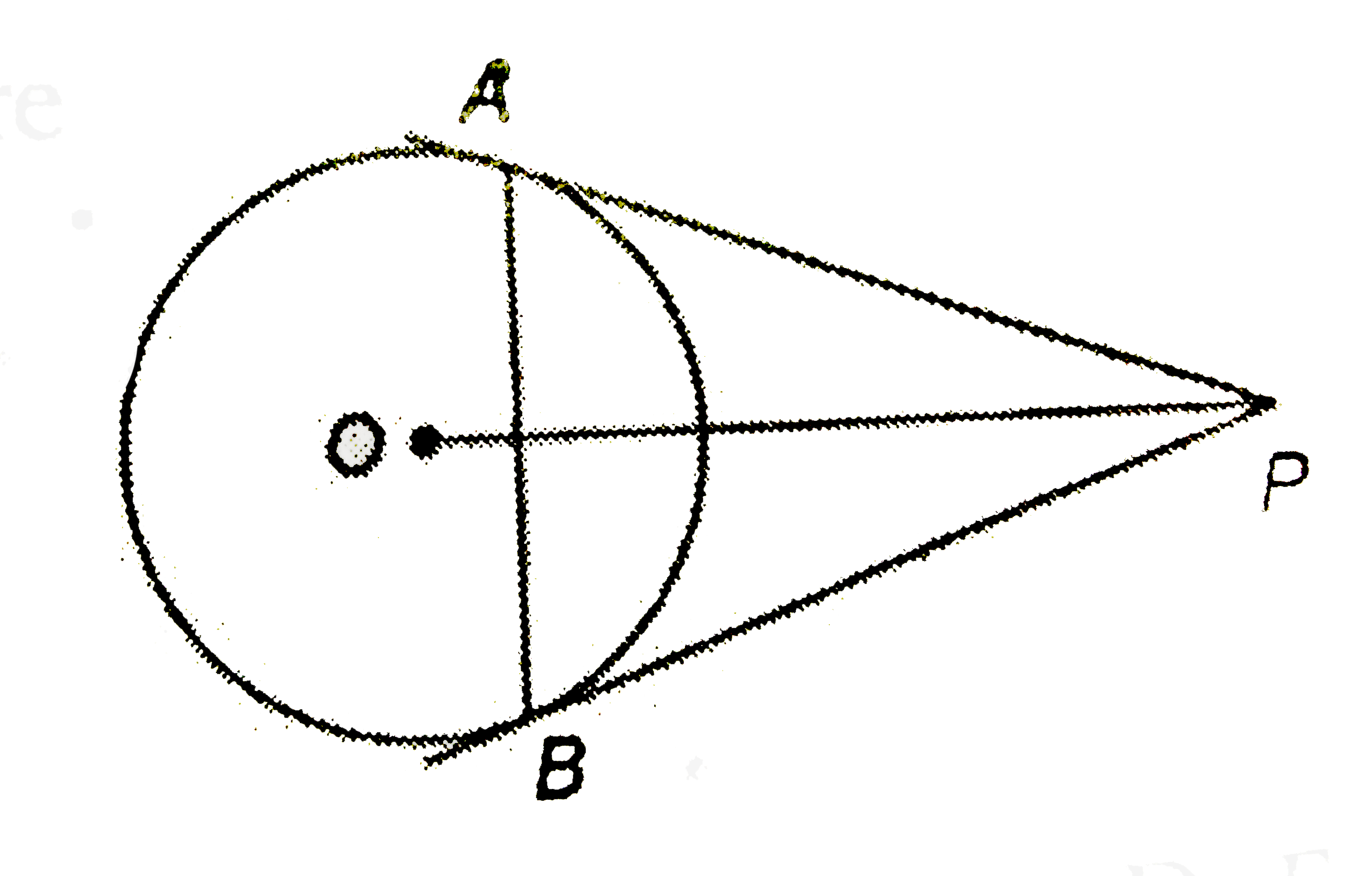
From a point P two tangents PA and PB are drawn to a circle with centre O. If OP is the diameter of the circle show that ∆APB is equilateral.
From the question we have:PA and PB are the tangents to the circle. ∴ OA ⊥ PA ⇒ ∠OAP = 90° In ΔOPA sin ∠OPA = OA OP = r 2r [Given OP is the diameter of the circle] ⇒ sin ∠OPA = 1 2 = sin 30 ⁰⇒ ∠OPA = 30°Similarly it can be proved that ∠OPB = 30°.Now ∠APB = ∠OPA + ∠OPB = 30° + 30° = 60°In ΔPAB PA = PB [length of tangents drawn from an external point to a circle are equal]⇒∠PAB = ∠PBA ............1 [Equal sides have equal angles opposite to them]∠PAB + ∠PBA + ∠APB = 180° [Angle sum property]⇒∠PAB + ∠PAB = 180° – 60° = 120° [Using 1]⇒2∠PAB = 120°⇒∠PAB = 60° .............2From 1 and 2∠PAB = ∠PBA = ∠APB = 60°∴ ΔPAB is an equilateral triangle.
Related Solutions
From a point , two tangents and are drawn to a circle with centre . If diameter of the circle, show that is equilateral.
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O. If OP is equal to diameter of the circle, then is
View SolutionFrom a point P two tangents PA and PB are drawn to a circle with centre O.if OP is equal to diameter of the circle then is
View Solutionएक वृत्त C(O, r) पर एक बिन्दु P से दो स्पर्शियाँ PA व PB खींची गयी है । यदि OP = 2r । सिद्ध कीजिए कि एक समबाहु त्रिभुज है।
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle C(0,r). If OP = 2r , show that ∆APB is equilateral.
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O and radius r. If OP=2r, show that is equilateral.
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O and radius r. If OP=2r, show that is equilateral.

View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O. If OP is equal to diameter of the circle then is___
View Solutionवृत्त के बाहर बिंदु से और दो स्पर्श रेखाएँ खींची गई हैं| दिखाएँ कि यदि , तो समबाहु त्रिभुज हैं|
View SolutionFrom a point P two tangents are drawn to a a circle with center o.if OP= diameter of the circle,show /_APB is equilateral.
View SolutionFrom a point , two tangents and are drawn to a circle with centre . If diameter of the circle, show that is equilateral.
View SolutionTwo tangents PA and PB are drawn to a circle with centre O from an external point P. Prove that
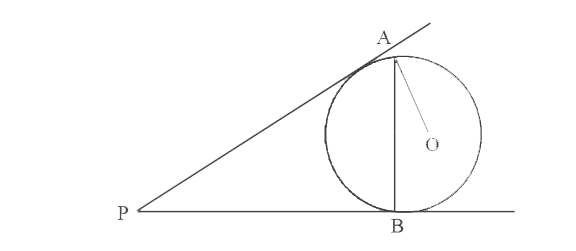
View SolutionPA and PB are the two tangents drawn on a circle from and external point P. The centre of the circle is O and the tangents touches the circles at points A and B. Then quadrilateral OAPB is-
View Solutionकिसी P बिंदु से, O केंद्र वाले वृत्त पर PA तथा PB को स्पर्श रेखाएं खींची जाती हे| यदि OP वृत्त के व्यास के बराबर हे, तो का मान बताये|
View SolutionO வை மையமாக உடைய வட்டத்திற்கு வெளியே உள்ள புள்ளி P யிலிருந்து வரையப்பட்ட தொடுகோடுகள் PA மற்றும் PB ஆகும் APB = எனில் AOB -யின் மதிப்பு காண்க ?
View SolutionFrom a point outside a circle with centre , tangents and are drawn to the circle. Prove that is the right bisector of the line segment .
View SolutionPA and PB are tangents to a circle with centre O, from a point P outside the circle and A and B are points on the circle. If , then is equal to
View SolutionTwo tangents PA and PB are drawn from a point P to the circle. If the radius of the circle is 5 cm and AB = 6 cm and O is the centre of the circle. OP cuts AB at C and OC = 4 cm, then OP :-
View Solutionएक वृत्त C(O, r) के बाह्य बिंदु P से वृत्त पर PA और PB दो स्पर्श रेखाएँ इस प्रकार खींची गई हैं कि है। सिद्ध करो कि
View SolutionTwo tangents PA and PB are drawn to circle with centre O from an external point P. Prove that
View Solution