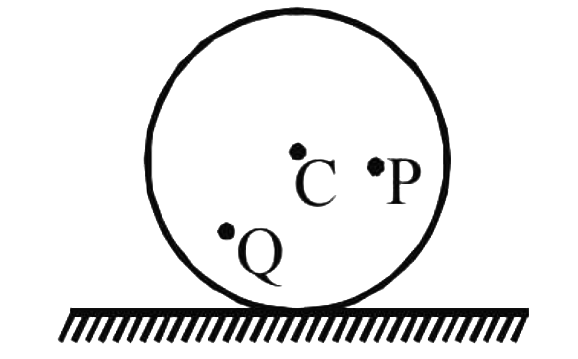
A disc is rolling without slipping on a horizontal surface. C is its centre and Q and P are two points equidistance from C. Let vP vQ and vC be the magnitudes of velocities of P Q and C respectivelya vQ > vC > vP b vQ vp
The correct Answer is:Option a
Correct Option a vQ > vC > vP Explanation :The rolling without slipping about O is shown in figure. From figure OQ > OC > OPWe know that v = rωvQ> vC>vP
Related Solutions
A disc is rolling (without slipping) on a horizontal surface. C is its center and Q and P are two points equidistant from C. to suppose V_P, V_Q And V_C are the magnitudes of the velocities of the points P, Q and C respectively, then
View SolutionA disc is rolling without slipping on a horizontal surface with C, as its centre and Q and P the two points equidistant from C. Let be the magnitudes of velocities of point P,Q and C respectively, then

View SolutionA disc is rolling without slipping on a horizontal surface with C, as its centre and Q and P the two points equidistant from C. Let v_(P),v_(Q) and v_(C) be the magnitudes of velocities of point P,Q and C respectively, then
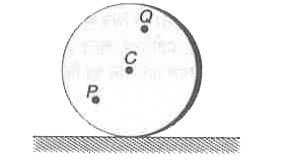
View SolutionA disc is rolling without slipping with angular velocity . P and Q are two points equidistant from the centre C. the order of magnitude fo velocity is
View SolutionA disc is rolling without slipping with angular velocity omega . P and Q are two points equidistant from the centre C. the order of magnitude fo velocity is
View SolutionA disc is rolling (without slipping) on a horizontal surface. C is its center and Q and P are two points equidistant from C . Let V_(P), V_(Q) and V_(C) be the magnitude of velocities of points P, Q and C respectively, then .
View SolutionA disc is rolling (without slipping) on a horizontal surface. C is its center and Q and P are two points equidistant from C . Let V_(P), V_(Q) and V_(C) be the magnitude of velocities of points P, Q and C respectively, then .
View SolutionA disc is rolling (without slipping) on a horizontal surface. C is its centre and Q and P are two point equidistance from C. let upsilon_(p),upsilon_(Q) and upsilon_(C) be the magnitude of velocities of points P, Q, and C repsectively, (a). upsilon_(Q)gtupsilon_(C)gtupsilon_(P) (b). upsilon_(Q)ltupsilon_(C)ltupsilon_(P) (c). upsilon_(Q)=upsilon_(P),upsilon_(C)=(1)/(2)upsilon_(P) (d). upsilon_(Q)ltupsilon_(C)gtupsilon_(P)
View SolutionW : VQ : : P :_____ |
View SolutionA disc is rolling (without slipping) on a horizontal surface. C is its centre and Q and P are two point equidistanec from C. let upsilon_(p),upsilon_(Q) and upsilon_(C) be the magnitude of velocities of points P, Q, and C repsectively, (a). upsilon_(Q)gtupsilon_(C)gtupsilon_(P) (b). upsilon_(Q)ltupsilon_(C)ltupsilon_(P) (c). upsilon_(Q)=upsilon_(P),upsilon_(C)=(1)/(2)upsilon_(P) (d). upsilon_(Q)ltupsilon_(C)gtupsilon_(P)
View Solution~(p^^) to [~p vv(~p vq)] Is equal
View SolutionThe vapour pressure of a dilute solution of non-volatile solute is and the of a pure solvent is . The lowering of the is
View SolutionThe vapour pressure of a dilute solution of non-volatile solute is and the of a pure solvent is . The lowering of the is
View SolutionThe vapour pressure of a dilute solution of non-volatile solute is and the of a pure solvent is . The lowering of the is
View SolutionA circular disc is rolling with a uniform angular speed W on a horizontal plane without slipping. The center of the disc is c and there are two points P and Q at equal distances from c. If the magnitudes of the velocities of the points P, C and R at any instant are v_(P) , v_(C) And v_(Q) are, then-
View Solutionएक वृत्ताकार डिस्क एक क्षैतिज तल पर बिना फिसले एकसमान कोणीय चाल से लुढ़क रही है। डिस्क का केंद्र C है तथा C से समदूरस्थ बिंदु Q तथा P है। यदि व C के वेगों के परिमाण क्रमशः तथा हैं तब
View SolutionThe vapour pressure of a dilute solution of non-volatile solute is and the of a pure solvent is . The lowering of the is
View SolutionThe vapour pressure (VP) of a dilute solution of non-volatile solute is P and the VP of pure solvent is the lowering of the VP is :
View SolutionThe vapour pressure (VP) of a dilute solution of non-volatile solute is P and the VP of pure solvent is the lowering of the VP is :
View SolutionW=VQ , define?
View Solution